 (分配関数)
(分配関数)  エントロピー, 自由エネルギー,
etc.
エントロピー, 自由エネルギー,
etc.分子の並進, 回転, 振動, etc.  (分配関数)
(分配関数)  エントロピー, 自由エネルギー,
etc.
エントロピー, 自由エネルギー,
etc.
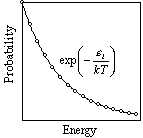 |
| 図 6.1 ボルツマン分布 |
6.1 ボルツマン分布
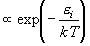
 i : 状態 i
のエネルギー
i : 状態 i
のエネルギー
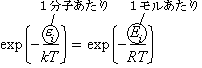
ex.) Br2 分子を振動励起状態 ( = 1)
と基底状態 (
= 1)
と基底状態 ( = 0) の存在比
= 0) の存在比
= exp(-h 10 / kT )
= 0.21 (at T = 298 K,
10 / kT )
= 0.21 (at T = 298 K, 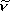 10
= 323 cm-1)
10
= 323 cm-1)
状態 i の多重度 gi を含めると、状態
i にある分子数 ni は
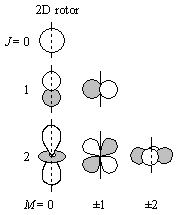 |
| 図 6.2 回転波動関数と多重度 |
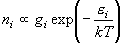 (6.1)
(6.1)
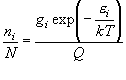 (6.2)
(6.2)
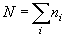 (総分子数)
(総分子数)
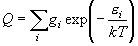 (分配関数)
(分配関数)
振動 : 多重度 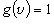
回転 : 多重度 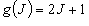 (二次元回転; 直線分子)
(二次元回転; 直線分子)
 回転分布
回転分布
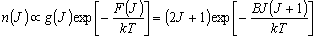
問題 6.1
1) I2 分子の振動 (= 213 cm-1) を調和振動子と仮定し、
= 0 の存在比を 1 としたときの、室温 (298 K) における、
= 1, 2, 3, 4 の準位の存在比を求めよ。
2) 剛体回転子近似のもとに、室温 (298 K) における HI 分子 (B = 6.5 cm-1) の回転分布を求めよ。 (J = 0 を 1 として存在比が 0.2 以下になる J まで計算せよ)
note:,
補足-波数単位の換算
6.2 統計力学的裏付
[配置と重率]
ex-1) 4 つの調和振動子が合計
3h のエネルギーを持つ場合
のエネルギーを持つ場合
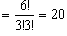
 )
の分子の数が n 0, n 1,
n 2, n 3
)
の分子の数が n 0, n 1,
n 2, n 3
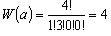 ,
,
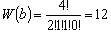 ,
,
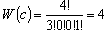
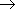 配置 b が最優勢配置
配置 b が最優勢配置
 |
| 図 6.3 配置と重率 (a) 4 つの箱 - 3 つの球 |
 のエネルギー
のエネルギー
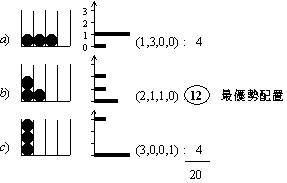
 |
| 図 6.3 配置と重率 (b) 7 つの箱 - 4 つの球 |
 のエネルギー
のエネルギー
 ボルツマン分布
ボルツマン分布
 |
| 図 6.3 配置と重率 (b) n 個の箱 - m 個の球 |
[ボルツマン分布の導出]
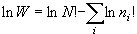 (6.3)
(6.3)
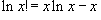
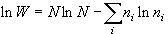 (6.4)
(6.4)
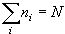 ,
,
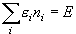 のもとでの lnW の最大値
(未定乗数法を使う)
のもとでの lnW の最大値
(未定乗数法を使う)
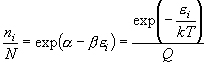 (6.5)
(6.5)