モルあたりの量への変換 :
 NA, k
NA, k 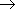 R
R
* ここではすべて1分子あたりの量
モルあたりの量への変換 :NA, k
R
8.1 簡単な系の熱力学関数
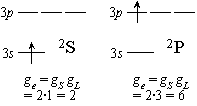 |
| 図 8.1 Na の電子状態 |
[Na原子]
Na 原子の基底状態 2S と (D線)励起状態 2 P の平衡定数 :
| S | L | ge = (2S + 1)(2L + 1) | ||
|---|---|---|---|---|
| 2S | 1/2 | 0 | 2  1 = 2 1 = 2 |
(図 8.1) |
| 2P | 1/2 | 1 | 2  3 = 6 3 = 6 |
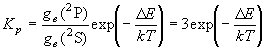 (8.1)
(8.1)
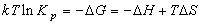 (8.2)
(8.2)

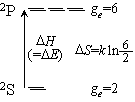 |
図 8.2 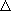 H と H と
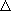 S S |
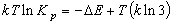 (8.3)
(8.3)
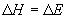 ,
,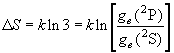 (8.4)
(8.4)

・低温では Kp << 1, 高温では
Kp 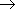 3
(T
3
(T 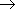
 )
)
・2P : エネルギー的に不利 (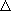 H
> 0)、エントロピー的には有利 (
H
> 0)、エントロピー的には有利 (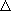 S
> 0)
S
> 0)
[一般の平衡定数]
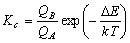 (7.1)
(7.1)
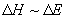 ,
,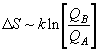 (8.5)
(8.5)

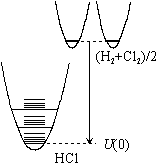 |
| 図 8.3 内部エネルギーの基準 |
8.2 内部エネルギー
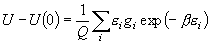
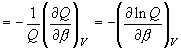 (8.6)
(8.6)
 = 1 / kT
= 1 / kT
分子運動からの寄与
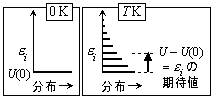 |
| 図 8.4 内部エネルギー |
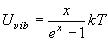 (8.a1)
(8.a1)
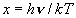 )
)
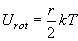 (8.a2)
(8.a2)
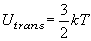 (8.a3)
(8.a3)
| ex.) | 室温 (298 K) における非直線分子 (r = 3) : Utrans + Urot = 3kT = 7.4 kJ mol-1 |
| ex.) | H2 と I2 (振動数: 4162, 214.6 cm-1)
の振動エネルギー (298 K) : Uvib (H2) = 7.8  10-6 cm-1 = 9.3
10-6 cm-1 = 9.3  10-8 kJ mol-1
10-8 kJ mol-1Uvib (I2) = 118.0 cm-1 = 1.4 kJ mol-1 |
8.3 エントロピー
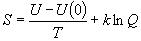 (8.7)
(8.7)分子運動からの寄与
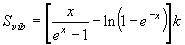 (8.a4)
(8.a4)
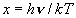 )
)
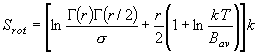 (8.a5)
(8.a5)
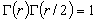 (直線分子),
(直線分子), 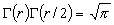 (非直線分子)
(非直線分子)
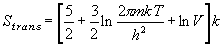 (8.a6)
(8.a6)
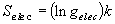 (8.a7)
(8.a7)
| ex.) | 1H2 と
127I2 (B : 59.3, 0.0374 cm-1 /
振動波数: 4162, 214.6 cm-1) の 298 K, 1 atm におけるエントロピー | ||
Svib (H2) = 3.3  10-7
10-7 |
Svib (I2) = 8.4 | [J K-1 mol-1] | |
| Srot (H2) = 13.0 | Srot (I2) = 74.2 | ||
| Strans (H2) = 117 | Strans (I2) = 178 | ||
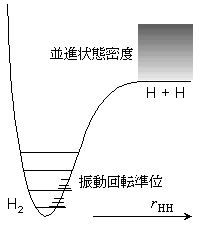 |
| 図 8.5 H2 の解離平衡 |
| ex.) | H2 解離平衡 @ 1000 K, p = 1 atm | ||||||
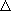 H / kT
= H / kT
= |
+ 51.96 | - 0.015 | - 1 | + 1.5 | + 1 | = 53.44 | |
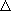 U (0) U (0)(= 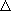 E ) E ) |
Uvib | Urot | Utrans | pV (= kT ) | |||
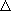 S / k = S / k = |
- 0.018 | - 2.77 | + 15.08 | + 1.39 | = 13.68 | ||
| Svib | Srot | Strans | Selec | ||||
| -lnKp = | 39.76 | ||||||
| Kp = | 5.40  10-18 [atm] 10-18 [atm] | ||||||
| ・H + H はエンタルピー的に不利, エントロピー (主に並進) 的に有利 | |||||||
8.4 他の熱力学関数
| ヘルムホルツ関数 | 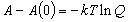 |
(8.a8) |
| エンタルピー | 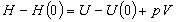 |
(8.a9) |
| ギブス関数 | 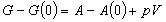 |
(8.a10) |
問題 8.1
1) 298 K における、気相反応 H2 + I2 2 HI の振動・回転・並進・電子状態のエントロピー変化 (
Svib /k ,
Srot /k ,
Strans /k ,
Selec /k ) を以下の情報から計算せよ。
H2 I2 HI 振動波数 [cm-1] 4162 213 2230 回転定数 B [cm-1] 59.3 0.0373 6.43 回転対称数 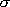
2 2 1 質量 m [amu] 2 254 128 電子状態の多重度 1 1 1
2) 上の結果と下の標準生成エンタルピーの値から、298 K におけるこの反応の平衡定数を求めよ。
H2 I2(g) HI Hf
(298 K)
/ kJ mol-10 62.42 26.50