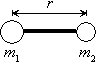
3.1 剛体回転子近似
 |
| 図 3.1 剛体回転子モデル |
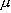 : 換算質量 - (2.3) 式]
: 換算質量 - (2.3) 式]
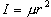 (3.1)
(3.1)
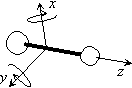 |
| 図 3.2 直線分子 = 二次元回転子 |
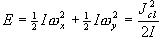 (3.2)
(3.2)
 x)2 +
(I
x)2 +
(I y)2
y)2
 |
| 図 3.3 回転エネルギー準位 |
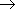 量子化
量子化[エネルギー準位]
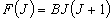 ,
J = 0, 1, 2, ... (3.3)
,
J = 0, 1, 2, ... (3.3)
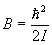 (エネルギー単位)
(3.4a)
(エネルギー単位)
(3.4a)
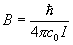 (波数単位)
(3.4b)
(波数単位)
(3.4b)
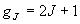 (3.5)
(3.5)
許容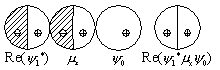 |
禁制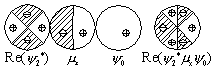 |
| 図 3.4 純回転遷移の選択則 (一次元回転子) |
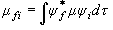 (3.6)
(3.6)
永久双極子モーメントを持つ
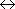 純回転遷移活性
純回転遷移活性
ex.) 等核二原子分子 (N2, O2, etc.) :
不活性
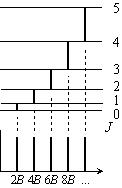 |
| 図 3.5 純回転遷移スペクトル |
[選択則] - 補足
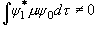 ,
,
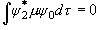
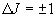 (3.7)
(3.7)
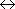 J 遷移波数
J 遷移波数
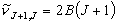 (3.8)
(3.8)
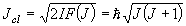
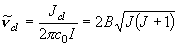
純回転遷移間隔 = 2B
例題 3.1 12C16O の遠赤外吸収スペクトルから 結合距離 r を求めよ
4,3 = 8B = 15.38 cm-1
B = 1.9225 cm-1 [(3.10)式]
I = 8.7686 amu2 [(3.4b)式],
= 6.8562 amu [(2.3)式]
r = 1.1309[(3.1)式]
10,9 = 20B = 38.41 cm-1)
B = 1.9205 cm-1
I = 8.7777 amu2 r = 1.1315
1 amu (原子質量単位) = 1
10-3 / NA [kg]
m(C) = 12 amu, m(O) = 15.9949 amu
1= 10-10 m
* J
大で r
大 となるのは、遠心歪のため
問題 3.1 オリオン星雲から観測される 86243.28 MHz のマイクロ波は 振動励起状態 (= 1) の 28Si16O の J = 2
1 遷移である。これからこの状態の SiO の核間距離を求めよ。
3.3 回転ラマン散乱
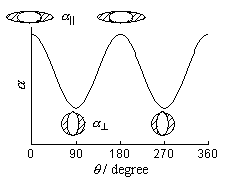 |
| 図 3.6 二原子分子回転と分極率 |
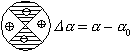 |
| 図 3.7 分極率の異方成分 |
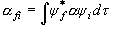 (3.9)
(3.9)
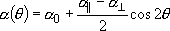 (3.10)
(3.10)
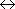 回転ラマン活性
回転ラマン活性
[選択則] - 補足
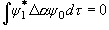 ,
,
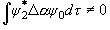
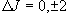 (3.11)
(3.11)
禁制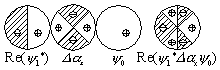 |
許容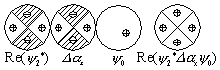 |
| 図 3.8 回転ラマン選択則 |
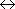 J ラマンシフト波数
J ラマンシフト波数
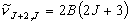 (3.12)
(3.12)
 2
2
回転ラマン散乱間隔 = 4B
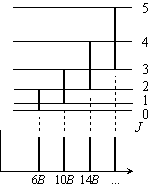 |
| 図 3.9 回転ラマン散乱スペクトル |
問題 3.2 H2 分子の核間距離は 0.742である。これから H2 (1H1H) および D2 (2H2H) 分子の回転ラマンスペクトルの間隔を予想せよ。
3.4 振動−回転スペクトル
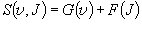
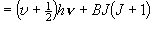 (3.13)
(3.13)
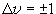 ,
,
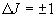 (3.14)
(3.14)
 =
1
=
1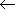 0]
0]
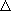 J = -1] :
J = 0
J = -1] :
J = 0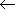 1, 1
1, 1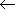 2, ... :
P(1), P(2), ...
2, ... :
P(1), P(2), ...
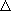 J = +1] :
J = 1
J = +1] :
J = 1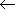 0, 2
0, 2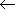 1, ... :
R(0), R(1), ...
1, ... :
R(0), R(1), ...
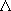
 0 の場合
0 の場合
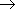 Q 枝
[
Q 枝
[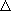 J = 0] も許容 [ ex.)
NO(2
J = 0] も許容 [ ex.)
NO(2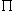 ) ]
) ]
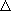 J = 0] :
J = 0
J = 0] :
J = 0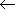 0, 1
0, 1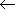 1, ... :
Q(0), Q(1), ...
1, ... :
Q(0), Q(1), ...
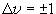 ,
,
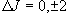 (3.15)
(3.15)
 =
1
=
1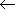 0]
0]
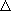 J = -2] :
J = 0
J = -2] :
J = 0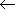 2, 1
2, 1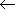 3, ... :
O(2), O(3), ...
3, ... :
O(2), O(3), ...
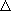 J = +2] :
J = 2
J = +2] :
J = 2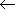 0, 3
0, 3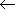 1, ... :
S(0), S(1), ...
1, ... :
S(0), S(1), ...
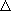 J J | -2 | -1 | 0 | +1 | +2 |
| スペクトル枝 | O | P | Q | R | S |
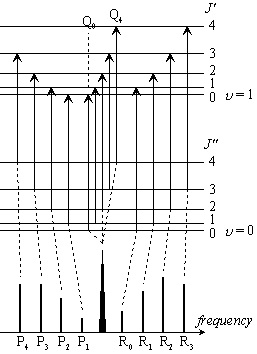 |
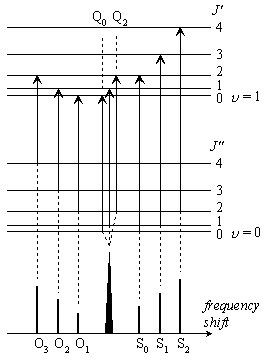 |
| 図 3.10 スペクトル枝 (IR) | 図 3.11 スペクトル枝 (Raman) |