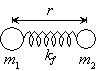
モデル
 |
| 図 2.1 調和振動子 モデル |
2.1 調和振動子近似
−モデル「分子 = ばねでつながった原子」
r : 核間距離, re : 平衡核間距離
x : 変位 (x = r - re),
kf : ばね定数
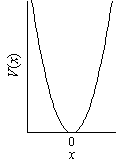 |
| 図 2.2 ポテンシャル |
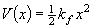 (2.1)
(2.1)
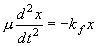 (2.2)
(2.2)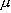 :
換算質量 (m1, m2 : 原子 1, 2 の質量)
:
換算質量 (m1, m2 : 原子 1, 2 の質量)
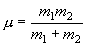 (2.3)
(2.3)
[振動数]
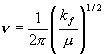 (2.4)
(2.4)
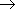 量子化
(cf. Atkins 12 章 - 振動運動)
量子化
(cf. Atkins 12 章 - 振動運動)
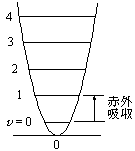 |
| 図 2.3 エネルギー準位 |
[エネルギー準位]
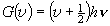 ,
,
 = 0, 1, 2, ... (2.5)
= 0, 1, 2, ... (2.5)
cf.) 赤外吸収周波数 = 分子振動周波数 / [ = 1
= 1  0 遷移]
0 遷移]
二原子分子の赤外吸収, cm-1 (m)
ばね定数 kf [N m-1] と結合次数,
HCl 2886 (3.47) NO 1876 (5.33) CO 2143 (4.67)
結合解離エネルギー D [kJ mol-1]
kf 結合次数 D HBr 384 1 366 Cl2 318 1 243 O2 1139 2 498 NO 1548 2.5 632 CO 1855 3 1076 N2 2241 3 945
例題 2.1 H35Cl の赤外吸収波数 2886 cm-1 から D35Cl (2H35Cl) の赤外吸収波数を推定せよ。
kf は核質量に依存しない. 波数比は-1/2 の比 [(2.4)式]. D35Clの赤外吸収波数 = 2886
(
DCl /
HCl)-1/2 = 2069 cm-1.
(実測値 2091 cm-1 との差は非調和性による)
問題 2.1 H37Cl, D37Cl の赤外吸収波数を推定せよ。
2.2 赤外振動遷移
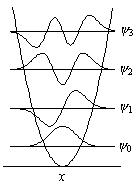 |
| 図 2.4 振動波動関数 |
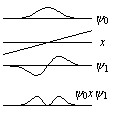 |
| 図 2.5a 許容遷移の
遷移モーメント |
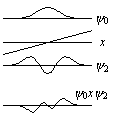 |
| 図 2.5b 禁制遷移の
遷移モーメント |
 ラマン散乱)
ラマン散乱)
[遷移双極子モーメント]
−吸収, 発光強度は「遷移双極子モーメント」に依存
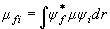 (2.6)
(2.6)
[赤外振動遷移]
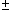
 q の電荷が局在)
q の電荷が局在)
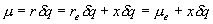 (2.7)
(2.7)
 = i
= i
 j )
j )
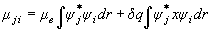
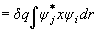 (2.8)
(2.8)
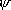 i と
i と
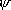 j は直交
(i
j は直交
(i  j )
j )
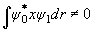 ,
,
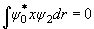
[選択則]
−遷移が起こるか否かを決定する規則
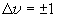 (2.9)
(2.9)
[赤外活性]
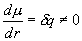 なら赤外活性 (2.10)
なら赤外活性 (2.10)
問題 2.2 調和振動子の= 1,
= 3 の波動関数を図示し、
= 3
1 の遷移が禁制であることを説明せよ。
2.3 振動ラマン散乱
ラマン散乱は分極率遷移 ( 赤外光学遷移)
赤外光学遷移)
[散乱モーメント]
−ラマン散乱強度は「散乱モーメント」に依存
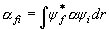 (2.11)
(2.11)
[振動ラマン散乱]
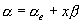 (2.12)
(2.12)
 = i
= i
 j )
j )
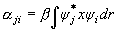 (2.13)
(2.13)
[選択則]
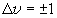 (2.14)
(2.14)
[ラマン活性]
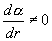 ならラマン活性 (2.15)
ならラマン活性 (2.15)
問題 2.3 N2 分子の 1) 双極子モーメント, 2) 分極率 が分子振動座標 x にどのように依存するかを示し、 赤外遷移・ラマン散乱が活性かどうかを判定せよ。