 |
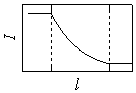
| 図 1.1 ランベルト-ベール則 |
1.1 ランベルト-ベール則
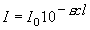 ,
,
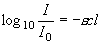 (1.1a)
(1.1a)
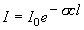 ,
,
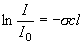 (1.1b)
(1.1b)
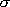 ,
,
 : 吸光係数 [次元: 濃度-1
長さ-1]
: 吸光係数 [次元: 濃度-1
長さ-1]
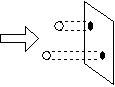 |
| 図 1.2 吸光断面積の古典的意味 |
[吸光係数]
 (底10): M-1
cm-1 (= dm3 mol-1 cm-1)
(底10): M-1
cm-1 (= dm3 mol-1 cm-1)
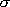 (底 e): (molecules
cm-3)-1 cm-1
= cm2 [molecule-1] 〜分子1個の影の面積
(底 e): (molecules
cm-3)-1 cm-1
= cm2 [molecule-1] 〜分子1個の影の面積
問題 1.1 あるカルボニル化合物 (推定吸光係数= 5〜20 dm3 mol-1 cm-1) の UV 吸収スペクトルを測定したい。測定セルの光路長は 1 cm であり、 分光光度計の雑音などから透過率 90% 以上や 5% 以下の吸収は 精度よく測定できない。測定試料はどの程度の濃度に調整すればよいか?
1.2 波長領域と分子運動
[地球温暖化] 加熱=太陽光 (可視: peak〜500 nm)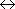 冷却=地球放射 (赤外: peak〜10
冷却=地球放射 (赤外: peak〜10 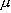 m)
大気は可視光に透明、赤外に分子吸収
m)
大気は可視光に透明、赤外に分子吸収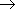 温室効果気体
温室効果気体注) GWP (Global Warming Potential / 温室効果ポテンシャル) は分子の赤外吸収によって主に決まるが、 放出された分子の大気中寿命にも依存する。
[波長領域]
| 紫外 | 10〜380 nm | 電子遷移 |
| 可視 | 380〜780 nm | 〃 |
| 赤外 | 780 nm〜300 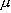 m m |
振動遷移〜回転遷移 |
| マイクロ波 | 300 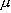 m〜1 m m〜1 m |
回転遷移 |
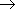 [Ne]3s03p1
[Ne]3s03p1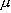 m)
m)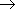 0 の遷移
0 の遷移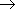 OH ラジカル生成源・オキシダント
OH ラジカル生成源・オキシダント[波長-周波数/波数/エネルギー]
| 記号 | 単位 | |
| 波長 | 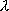 | nm,
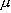 m (断らない限り真空中) m (断らない限り真空中) |
| 周波数 |  | s-1, Hz |
| 波数 | 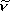 |
cm-1 |
| エネルギー |  ,
h ,
h | J (= J photon-1, or J molecule-1), kJ mol-1, cm-1 |
c0 : 真空中の光速 = 299792458 m s-1, NA : アボガドロ数 = 6.02213671023 mol-1
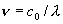 ,
,
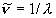 ,
,
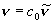
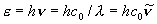 (1粒子あたり)
(1粒子あたり)
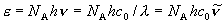 (1モルあたり)
(1モルあたり)
問題 1.2 35Cl2 を 330 nm で光分解した。分解直後の Cl 原子の飛行速度を求めよ。Cl-Cl 結合エネルギーは 242.6 kJ mol-1である。
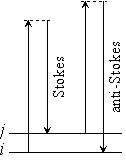 |
| 図 1.3 ラマン散乱 |
1.4 ラマン散乱
 I
と同じ周波数)
I
と同じ周波数)
 i j
だけシフト)
i j
だけシフト)
 scatter scatter |
=  I (レーリー散乱) I (レーリー散乱) |
=  I - I -
 i j (ラマン散乱,
ストークス光) i j (ラマン散乱,
ストークス光) | |
=  I + I +
 i j (ラマン散乱,
反ストークス光) i j (ラマン散乱,
反ストークス光) |
 ラマン散乱:分極率による
ラマン散乱:分極率による[分極率]
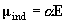 (1.2)
(1.2)