3.A 補足−回転量子化と回転準位の多重度

• 回転運動の量子化に関しては、Atkins 12 章 - 回転運動 (邦訳第６版では p. 353-, 第４版では p. 482-) を参照せよ。
• 紛らわしいことであるが、講義中で「二次元回転子」と呼ぶ、 直線分子の回転運動は、Atkins 12 章では「三次元の回転」に相当することに 注意せよ。

[多重度]

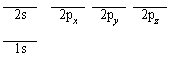図 3.a1 水素原子軌道エネルギー

• 回転運動の量子力学解に不慣れな場合は、その波動関数が水素原子の 「軌道」と類似であることに気づくと、理解しやすいかもしれない。
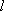• 水素原子の 1s 軌道 (方位量子数 = 0) は縮退していないが、2p 軌道 (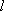 = 1) は 3 重に縮退している。このことは「電子の入れ物」が 2p_x, 2p_y, 2p_z の 3 通りあると解釈される。 一般に方位量子数 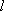の軌道は 2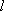 + 1 重に縮退している。 [例えば d 軌道 (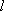 = 2) は 5 重縮退]
  
• 直線分子の回転運動の量子力学解は、水素原子軌道と似ている。 回転波動関数は球面調和関数である。水素原子の波動関数 (軌道) の角度方向の分布も球面調和関数であるが、動径方向にも分布を持つ点で、 回転波動関数とは異なる。
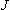• 回転量子数 = 0 の波動関数は 図 3.a2 の s 軌道と同じ「形」をしており、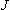 = 1, 2 の波動関数は、それぞれ p, d 軌道と同じである。 （異なる記号が使われるが回転運動の 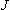も、 水素原子軌道の 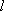も角運動量の量子数である）
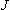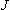• 回転量子数 の状態が 2 + 1 重に縮退していることは、水素原子の p, d 軌道が 3, 5 重に縮退していることと全く同様で、 異なる波動関数の状態が同じエネルギーを持つことに相当する。

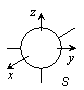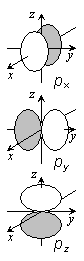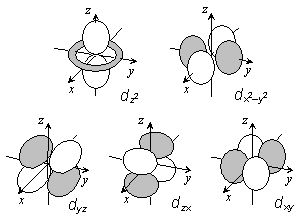s 軌道	p 軌道	d 軌道
図 3.a2 水素原子軌道の形