 3 - 6 = 3
3 - 6 = 3
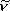 1 (OH伸縮) = 3436,
1 (OH伸縮) = 3436,
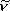 2 (変角) = 1392,
2 (変角) = 1392,
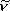 3 (OO伸縮) = 1098 [cm-1]
3 (OO伸縮) = 1098 [cm-1]
4.1 多原子分子の振動
 3 - 6 = 3
3 - 6 = 3
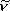 1 (OH伸縮) = 3436,
1 (OH伸縮) = 3436,
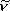 2 (変角) = 1392,
2 (変角) = 1392,
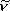 3 (OO伸縮) = 1098 [cm-1]
3 (OO伸縮) = 1098 [cm-1]
[基準振動]
 3 - 6 = 3
3 - 6 = 3
 3 - 5 = 4
3 - 5 = 4
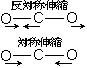 |
| 図 4.1 CO2 基準振動 |
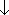
 独立
独立
| [cm-1] | |
| C-H 伸縮 | 〜3000 |
| C-C 伸縮 | 〜 900 |
| C=C 伸縮 | 〜1650 |
| C-C-H 変角 | 〜1000 |
| H-C-H 変角 | 〜1450 |
| 赤外 | ラマン | |
|---|---|---|
CO2  1
(対称伸縮) 1
(対称伸縮) | × | ○ |
CO2  2
(変角) 2
(変角) | ○ | × |
CO2  3
(反対称伸縮) 3
(反対称伸縮) | ○ | × |
CH4  1
(全対称C-H伸縮) 1
(全対称C-H伸縮) | × | ○ |
| N2 | × | ○ |
| HCl | ○ | ○ |
H2O  1
(対称伸縮) 1
(対称伸縮) | ○ | ○ |
H2O  3
(反対称O-H伸縮) 3
(反対称O-H伸縮) | ○ | ○ |
CH3  2
(変角-傘反転振動) 2
(変角-傘反転振動) | ○ | × |
[赤外活性・ラマン活性]
永久双極子を変化させる振動
(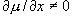 )
= 赤外活性
)
= 赤外活性
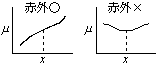
分極率を変化させる振動
(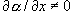 )
= ラマン活性
)
= ラマン活性
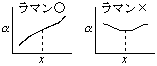
[選択則] (赤外・ラマン)
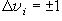 (4.2)
(4.2)
 1
(全対称C-H伸縮)
1
(全対称C-H伸縮) 2
(変角)
2
(変角) 1
(対称伸縮),
1
(対称伸縮),  3 (反対称伸縮)
3 (反対称伸縮)4.2 多原子分子の回転
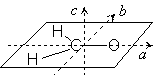 |
| 図 4.2 H2COの回転軸 |
[慣性モーメント]
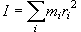 (4.3)
(4.3)
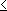 IB
IB 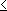 IC
IC
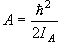 ,
,
 ,
,
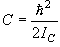 (4.4)
(4.4)
[エネルギー準位]
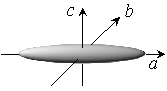 |
| 図 4.3a 偏長コマ |
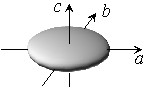 |
| 図 4.3b 偏平コマ |
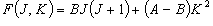 (4.5)
(4.5)
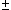 1,
1,
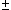 2, ...,
2, ..., 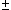 J
J
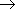 C
C
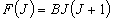 (4.6)
(4.6)
| 純回転遷移 | 回転ラマン | |
|---|---|---|
| N2 | × | ○ |
| HCl | ○ | ○ |
| CH4 | × | × |
| CH3 | × | ○ |
[純回転遷移・回転ラマン]
 永久双極子モーメントを持つ
永久双極子モーメントを持つ
 分極率に異方性がある
分極率に異方性がある
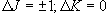 (4.7)
(4.7)
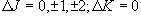 (4.8)
(4.8)
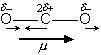
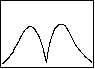 |
図 4.4a CO2
 3 バンド (平行遷移) 3 バンド (平行遷移) |
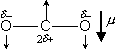
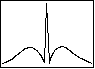 |
図 4.4b CO2
 2 バンド (垂直遷移) 2 バンド (垂直遷移) |
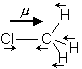
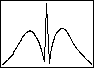 |
図 4.5a CH3Cl
 3 バンド (平行遷移) 3 バンド (平行遷移) |
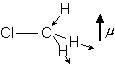
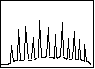 |
図 4.5a CH3Cl
 4 バンド (垂直遷移) 4 バンド (垂直遷移) |
4.3 振動回転スペクトル
[平行・垂直遷移]
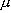 (遷移双極子) と z
(分子軸)が:
(遷移双極子) と z
(分子軸)が:
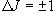 ... Q 枝× (4.9a)
... Q 枝× (4.9a)
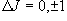 ... Q 枝○ (4.9b)
... Q 枝○ (4.9b)
 3 (反対称伸縮)
- 平行、
3 (反対称伸縮)
- 平行、 2 (変角) - 垂直
2 (変角) - 垂直
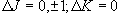 (4.10a)
(4.10a)
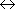 K" = 0
は
K" = 0
は 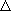 J =
J = 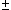 1 )
1 )
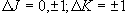 (4.10b)
(4.10b)
 3 (C-Cl 伸縮)
- 平行、
3 (C-Cl 伸縮)
- 平行、 4 (CH3 縮退伸縮)
- 垂直
4 (CH3 縮退伸縮)
- 垂直
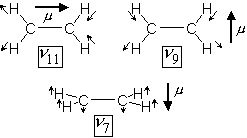 |
| 図 4.6 C2H4 の振動モード |
[a タイプ遷移(b タイプ・c タイプ)]
(非対称コマ分子) が a (b, c)
軸と平行 ... a (b, c) タイプ
が a (b, c)
軸と平行 ... a (b, c) タイプ
 11 (CH2 対称伸縮)
... a タイプ
11 (CH2 対称伸縮)
... a タイプ
 9 (CH2 反対称伸縮)
... b タイプ
9 (CH2 反対称伸縮)
... b タイプ
 7 (CH2 縦揺)
... c タイプ
7 (CH2 縦揺)
... c タイプ
 3
バンドの回転線間隔, 〜10.0 cm-1, から C-H 結合距離を求めよ
(正四面体を仮定)
3
バンドの回転線間隔, 〜10.0 cm-1, から C-H 結合距離を求めよ
(正四面体を仮定)
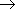 回転線間隔 = 2B.
回転線間隔 = 2B.
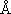 2
[(4.4) 式].
2
[(4.4) 式].
 .
.