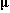
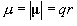 (10.1)
(10.1)
 10-30 C m
10-30 C m
 10-10 C
10-10 C
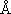 離れた -e と
e = 4.80321 D
離れた -e と
e = 4.80321 D
10.1 電気双極子モーメント
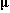
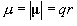 (10.1)
(10.1)
 10-30 C m
10-30 C m
 10-10 C
10-10 C
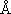 離れた -e と
e = 4.80321 D
離れた -e と
e = 4.80321 D
[永久双極子]
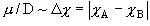 (10.2)
(10.2)
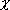 : 電気陰性度
: 電気陰性度
[誘起双極子]
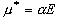 (10.3)
(10.3)
 : 分極率
: 分極率
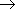
 大
大
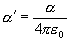 (10.4)
(10.4)
 0 : 真空の誘電率
0 : 真空の誘電率
10.2 マクロな物性−誘電率
[分極]
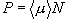 (10.5)
(10.5)
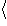
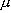
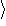 :
平均双極子モーメント, N : 分子数密度
:
平均双極子モーメント, N : 分子数密度
[高周波電場中の分極]
分子はランダムな配向をとる  外部電場がなければ流体では P = 0。(多くの固体でも同様)
外部電場がなければ流体では P = 0。(多くの固体でも同様)
 配向分極
配向分極 分子配向が電場に追随して揃うことによる分極。 <
1011 Hz
分子配向が電場に追随して揃うことによる分極。 <
1011 Hz
 変形分極
変形分極 原子核位置が電場に追随して変形することによる分極。 <
1013 Hz
原子核位置が電場に追随して変形することによる分極。 <
1013 Hz
 電子分極
電子分極 電子分布が電場に追随して変形することによる分極。
電子分布が電場に追随して変形することによる分極。
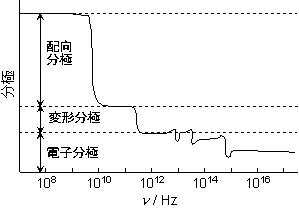 |
| 図 10.1 高周波電場による分極 |
[誘電率]
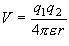 (10.6)
(10.6)
 : 誘電率
: 誘電率
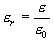 (10.7)
(10.7)
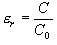 (10.8)
(10.8)
ミクロな量との関係
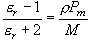 (10.9)
(10.9)
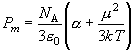 (10.10)
(10.10)
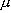 を無視)
を無視)
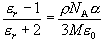 (10.11)
(10.11)
 |
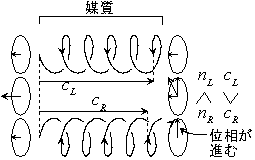
| 図 10.2 直線偏光 = 左円偏光 + 右円偏光 |
10.3 光学物性
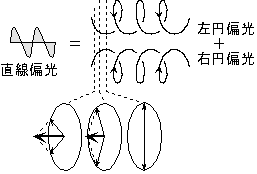
[屈折率]
 (10.12)
(10.12)
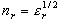 (10.13)
(10.13)
[光学活性]
偏光面を回転させる性質 :
円複屈折性 (右・左円偏光に対する屈折率の差異) による
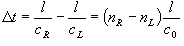 (10.14)
(10.14)
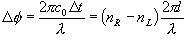 (10.15)
(10.15)
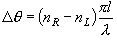 (10.16)
(10.16)
 |
| 図 10.3 旋光度 |
 r の測定値から Debye
式を仮定して、H2O 分子の双極子モーメント
r の測定値から Debye
式を仮定して、H2O 分子の双極子モーメント
 [D] と分極率体積
[D] と分極率体積
 '
[
'
[ 3 = 10-30
m3] を求めよ。
3 = 10-30
m3] を求めよ。温度 /  C C |
蒸気圧 / atm |  r r |
| 80 | 0.467 | 1.00305 |
| 100 | 1.000 | 1.00587 |