(c) 2001 by Akira Miyoshi. All rights reserved.
[Top]
[はじめに]
[1章]
[2章]
[3章]
[4章]
[5章]
[6章]
[7章]
[8章]
[9章]
[10章]
[11章]
2001 物理化学 II - 6章
6. ボルツマン分布
6.1 熱平衡状態
- 熱平衡にある分子集団 (カノニカルアンサンブル)
のエネルギー分布はボルツマン分布に従う
[ボルツマン分布]
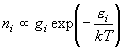 (6.1)
(6.1)
- ni : 状態 i にある分子数,
gi : 状態 i の多重度,
 i : 状態 i のエネルギー
i : 状態 i のエネルギー
- k : ボルツマン定数, T : 絶対温度
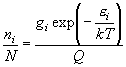 (6.2)
(6.2)
- N : 総分子数, Q : 分配関数 (規格化定数)
-
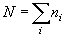 ,
,
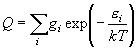
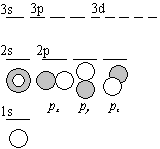 |
| 図 6.1 水素原子軌道 |
[多重度]
- = 縮重度、縮退数
- (異なる複数の状態が同じエネルギーに存在する)
- ex.) 水素原子軌道 (n : 主量子数, l : 方位量子数)
gn (殻縮重度) = n2,
gl (方位縮重度) = 2l + 1
- K 殻 (gn = 1): 1s(gl = 1)
- L 殻 (gn = 4): 2s(gl = 1),
2p(gl = 3)
- M 殻 (gn = 9): 3s(gl = 1),
3p(gl = 3), 3d(gl = 5)
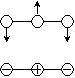
図 6.2 CO2 の
縮退変角振動 |
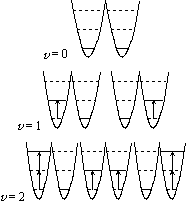
図 6.3 縮退振動の縮重度 |
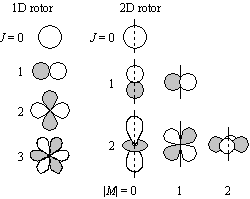
図 6.4 回転多重度 |
- ex.) CO2 縮退変角振動
xz, yz 平面上の変角 ... 縮退 (同エネルギー)
- g
 =
=
 + 1
+ 1
- ex.) 回転多重度
一次元回転 : gJ = 1 /
二次元回転 : gJ = 2J + 1
[ボルツマン分布の観測例]
- ex.) 酸素原子基底状態の微細構造分布
-
- 3P2, 3P1,
3P0 状態 : EJ = 0, 158.5, 226.5
cm-1, gJ = 2J + 1 = 5, 3, 1
- 298 K における存在比 : 74.3%, 20.7%, 5.0%
- ex.) CO の回転分布 (296 K)
-
- 赤外吸収の回転線強度分布
 回転分布
回転分布
- F (J ) = BJ (J + 1)
[B 〜 1.92 cm-1], gJ = 2J + 1
問題 6.1
1) I2 分子の振動エネルギー準位は 213.76
 - 0.596
- 0.596  2
[cm-1] で表される。
2
[cm-1] で表される。 = 0 の存在比を 1
としたときの、室温 (298 K) における、
= 0 の存在比を 1
としたときの、室温 (298 K) における、 =
1, 2, 3, 4 の準位の存在比を求めよ。
=
1, 2, 3, 4 の準位の存在比を求めよ。
2) 剛体回転子近似のもとに、室温 (298 K) における HI 分子の回転分布
(B = 6.5 cm-1) を求めよ。 (最大値を 1 として存在比が
0.05 以下になるJまで計算せよ)
6.2 統計力学的説明
[配置と重率]
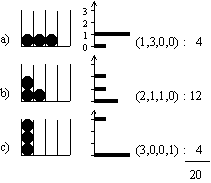 |
| 図 6.5 配置と重率 |
- ex.) 4 つの調和振動子が合計 3h
 のエネルギーを持つ場合
のエネルギーを持つ場合
- 総重率
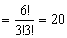
- 各配置の重率 :
-
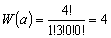
-
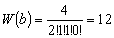
-
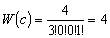
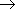 配置 b が最も起こりやすい
配置 b が最も起こりやすい
[ボルツマン分布]
= 分子数 N が十分大きい時の最確配置
- 配置 (n0, n1,
n2, ...) の対数重率
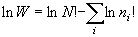 (6.3)
(6.3)
- + Stirling の近似 :
ln x ! = x ln x - x
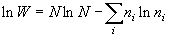 (6.4)
(6.4)
- 束縛条件
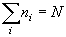 ,
,
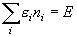 のもとでの lnW の最大値
(未定乗数法を使う)
のもとでの lnW の最大値
(未定乗数法を使う)
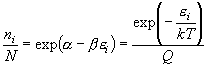 (6.5)
(6.5)
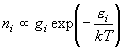 (6.1)
(6.1)
 i : 状態 i のエネルギー
i : 状態 i のエネルギー
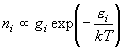 (6.1)
(6.1)
 i : 状態 i のエネルギー
i : 状態 i のエネルギー
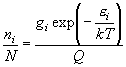 (6.2)
(6.2)
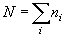 ,
,
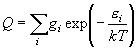




 =
=
 + 1
+ 1
 回転分布
回転分布
 - 0.596
- 0.596  2
[cm-1] で表される。
2
[cm-1] で表される。 = 0 の存在比を 1
としたときの、室温 (298 K) における、
= 0 の存在比を 1
としたときの、室温 (298 K) における、 =
1, 2, 3, 4 の準位の存在比を求めよ。
=
1, 2, 3, 4 の準位の存在比を求めよ。
 のエネルギーを持つ場合
のエネルギーを持つ場合
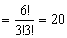
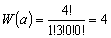
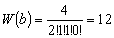
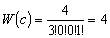
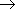 配置 b が最も起こりやすい
配置 b が最も起こりやすい
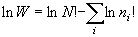 (6.3)
(6.3)
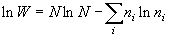 (6.4)
(6.4)
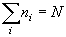 ,
,
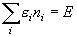 のもとでの lnW の最大値
(未定乗数法を使う)
のもとでの lnW の最大値
(未定乗数法を使う)
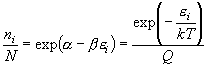 (6.5)
(6.5)