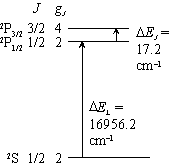
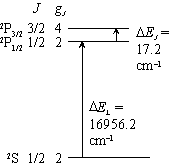 |
| 図 7.1 Na 原子 |
7.1 化学平衡
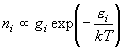 (6.1)
(6.1)
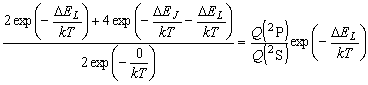
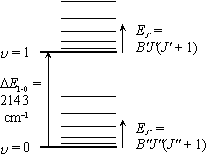 |
| 図 7.2 CO 分子 |
 = 1 状態の振動基底状態
(
= 1 状態の振動基底状態
( = 0) 対する存在比
= 0) 対する存在比
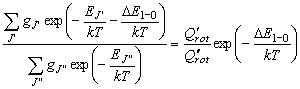
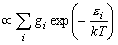 = 分配関数
= 分配関数
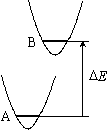 |
| 図 7.3 平衡定数 |
[化学平衡定数]
![K_c = \frac{{[B]_e }}{{[A]_e }} = \frac{{\sum\nolimits_B
{g_i \exp \left( { - \frac{{\varepsilon _i }}{{kT}} -
\frac{{\Delta E}}{{kT}}} \right)} }}{{\sum\nolimits_A {g_i
\exp \left( { - \frac{{\varepsilon _i }}{{kT}}} \right)} }} =
\frac{{Q_B }}{{Q{}_A}}](eqn/eq07_nn4.gif)
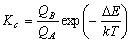 (7.1)
(7.1)
7.2 分子分配関数
[振動分配関数]
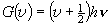 ,
,
 = 0, 1, 2, ... (2.5)
= 0, 1, 2, ... (2.5)
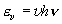 ,
,  = 0, 1, 2, ... (7.2)
= 0, 1, 2, ... (7.2)
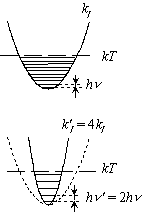 |
| 図 7.4 古典近似の振動分配関数 |
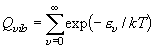 ... 等比級数
... 等比級数
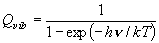 (7.3)
(7.3)
 <<
kT ) の振動分配関数
<<
kT ) の振動分配関数

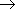 分配関数小
分配関数小
[回転分配関数]
二次元回転子
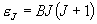 , J = 0, 1, 2,
... (3.3)
, J = 0, 1, 2,
... (3.3)
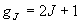 (3.5)
(3.5)
![Q_{rot}^{{\rm 2D}} = \sum\limits_J {g_J \exp \left[
{ - \varepsilon _J /kT} \right]}](eqn/eq07_nn6.gif)
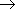 積分
積分
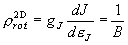
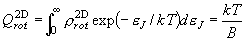
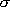 を考慮
を考慮
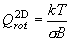 (7.4)
(7.4)
三次元回転子・一次元回転子
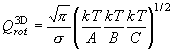 (7.5)
(7.5)
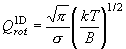 (7.6)
(7.6)
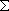 g-
(振動数 1580, B = 1.44 cm-1) と励起状態
A 3
g-
(振動数 1580, B = 1.44 cm-1) と励起状態
A 3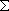 u+
(振動数 799, B = 0.91 cm-1) の 298 K における平衡定数を
(電子励起エネルギーを無視して) 求めよ。
u+
(振動数 799, B = 0.91 cm-1) の 298 K における平衡定数を
(電子励起エネルギーを無視して) 求めよ。
[回転対称数 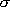 ]
]
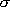 : : |
等価な原子を区別した場合に区別できる配置うち、 分子回転によって交換可能な配置の数 |
ex.) H2:Ha-Hb
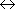 Hb-Ha ...
Hb-Ha ...
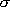 = 2
= 2
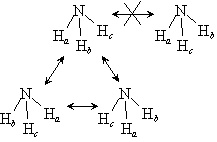
ex.) NH3 (ピラミッド型) : 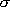 = 3
(図 7.5)
= 3
(図 7.5)
ex.) CH3 (平面三角形) : 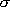 = 6
(図 7.6)
= 6
(図 7.6)
 |
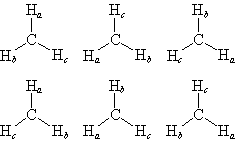 |
| 図 7.5 NH3 の回転対称数 | 図 7.6 CH3 の回転対称数 |