 点電荷
点電荷
 点電荷
点電荷
9.1.1 正八面体 (Oh) 6配位錯体
 金属 d 軌道の静電場分裂
金属 d 軌道の静電場分裂 不安定化
(eg : +3/5
不安定化
(eg : +3/5  O)
O)
 安定化
(t2g : -2/5
安定化
(t2g : -2/5
 O)
O)
 O :
配位子で決まる結晶場分裂パラメータ
(
O :
配位子で決まる結晶場分裂パラメータ
( d-d 遷移吸収)
d-d 遷移吸収) O
O
<高スピン・低スピン錯体>
| 低スピン | 高スピン | ||
| eg |   |
 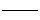 |
|
| t2g | 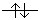 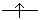
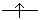 |
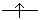 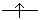
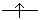 | |
| LFSE | -1.6  O O |
-0.6  O O | |
| Eex | -3 K | -6 K |
 O - 3 K
O - 3 K
 O > 3 K :
低スピン錯体が安定
O > 3 K :
低スピン錯体が安定
 O < 3 K :
高スピン錯体が安定
O < 3 K :
高スピン錯体が安定
 O 小
O 小
 高スピン錯体が安定
高スピン錯体が安定
 O 大
O 大
 低スピン錯体が安定
低スピン錯体が安定
| 電子配置 | E (高スピン) | E (低スピン) | E (高スピン) - E (低スピン) |
| d4 | - 0.6  O - 6 K O - 6 K |
- 1.6  O - 3 K O - 3 K |
 O - 3 K O - 3 K |
| d5 | - 10 K | - 2  O - 4 K O - 4 K |
2  O - 6 K O - 6 K |
| d6 | - 0.4  O - 10 K O - 10 K |
- 2.4  O - 6 K O - 6 K |
2  O - 4 K O - 4 K |
| d7 | - 0.8  O - 11 K O - 11 K |
- 1.8  O - 9 K O - 9 K |
 O - 2 K O - 2 K |
<磁気モーメント>
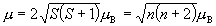
 1/2,
1/2,
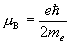 [ボーア磁子])
[ボーア磁子])
 基底状態のスピン多重度の決定
基底状態のスピン多重度の決定
| Ion | n | S | 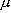 / /
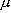 B (calc.) B (calc.) |
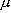 / /
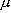 B (exp.) B (exp.) |
| Ti3+ | 1 | 1/2 | 1.73 | 1.7 - 1.8 |
| V3+ | 2 | 1 | 2.83 | 2.7 - 2.9 |
| Cr3+ | 3 | 3/2 | 3.87 | 3.8 |
| Mn3+ | 4 | 2 | 4.90 | 4.8 - 4.9 |
| Fe3+ | 5 | 5/2 | 5.92 | 5.9 |
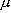 B であった。
B であった。9.1.2 正四面体(Td)4配位錯体
 安定化 (e : -3/5
安定化 (e : -3/5
 T)
T)
 不安定化
(t2 : +2/5
不安定化
(t2 : +2/5
 T)
T)
 T :
配位子で決まる
T :
配位子で決まる
 T <
T <
 O で弱い場
O で弱い場
 高スピンのみ
高スピンのみ
* 以下は本年度 (2001 年度) の講義では省略しました
 分子軌道
分子軌道
 分子軌道
分子軌道