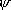 - =
- =
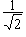 (
(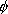 A -
A -
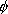 B)
B) u
u反結合性
ungerade (独)
= odd / 奇
(奇関数)
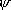 + =
+ =
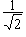 (
(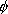 A +
A +
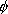 B)
B) g
g結合性
gerade (独)
= even / 偶
(偶関数)
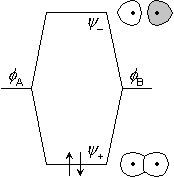
| 反転 i に | ||
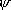 - = - =
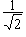 (
(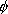 A - A -
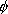 B) B) |
 u u反結合性 ungerade (独) = odd / 奇 |
反対称 (奇関数) |
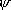 + = + =
 (
(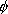 A + A +
 B) B) |
 g g結合性 gerade (独) = even / 偶 |
対称 (偶関数) |
< ,
,  ,
,
 軌道>
軌道>
| side view | head view | C v v対称種 |
D h h対称種 |
慣用表現 * = 反結合性 |
[ 軌道] 軌道] | ||||
 |
 |
 |
 g g |
s-s  |
 |
 |
 |
 u u |
s-s  * * |
 |
 |
 |
- | s-p  |
 |
 |
 |
 g g |
p-p  |
 |
 |
 |
 u u |
p-p  * * |
 |
 |
 |
 g g |
d-d  |
[ 軌道] 軌道] | ||||
 |
 |
 |
 u u |
p-p  |
 |
 |
 |
 g g |
p-p  * * |
 |
 |
 |
- | p-d  |
 |
 |
 |
 u u |
d-d  |
[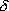 軌道] 軌道] | ||||
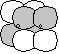 |
 |
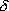 |
 g g |
d-d  |
 |
 |
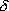 |
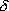 u u |
d-d 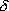 * * |
<節面と 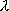 >
>
 軌道 軌道 |
 軌道 軌道 |
 軌道 軌道 | |
| 分子軸を含む節面数 | 0 | 1 | 2 |
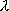 (l の分子軸への射影) (l の分子軸への射影) |
0 | 1 | 2 |
| エネルギー | 低  高 高 | ||
 直線分子軌道
直線分子軌道  ,
,
 ,
, 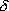 , ...
, ... ,
, 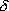 軌道では結合性軌道が
gerade
軌道では結合性軌道が
gerade 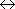
 軌道では
反 結合性軌道が gerade
軌道では
反 結合性軌道が gerade
<高次結合>
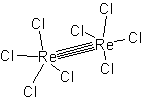
 四重結合
四重結合| 電子配置 : |  g2 g2 |
 u4 u4 |
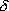 g2 g2 |
(d-d ) ) |
(2 d-d d-d ) ) |
(d-d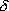 ) ) |
 h)
h)
6.3.1 O2の分子軌道 (MO)
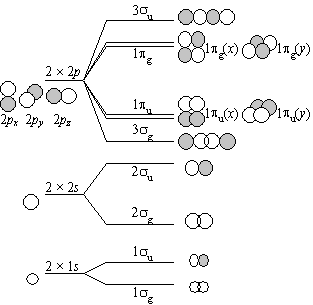
| 原子軌道 | 結合性 | 反結合性 | |
| 1s-1s | 1 g g |
1 u u |
内殻軌道 |
| 2s-2s | 2 g g |
2 u u |
内殻的 |
| 2pz-2pz | 3 g g |
3 u u |
重なり大 -分裂大 |
| 2px-2px 2py-2py |
1 u u |
1 g g |
重なり小 分裂小 (2重縮退) |
(同じ対称性の軌道 : 下から順に 1, 2, 3, ...)
電子配置 :
1 g2
1
g2
1 u2
2
u2
2 g2
2
g2
2 u2
3
u2
3 g2
1
g2
1 u4
1
u4
1 g2
g2
 電子はスピンが高くなる配置
電子はスピンが高くなる配置
 O2 の電子基底状態は三重項
[1
O2 の電子基底状態は三重項
[1 g(x)1
1
g(x)1
1 g(y)1]
(常磁性)
g(y)1]
(常磁性)
| S (スピン量子数) | 2S + 1 (スピン多重度) | ||
| 一重項 | 0 | 1 | |
| 三重項 | (1/2 + 1/2 =) 1 | 3 | 常磁性 |
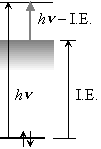
6.3.2 N2 の MO
 - I.E.
- I.E.
 軌道エネルギーの測定
軌道エネルギーの測定
 N2 の軌道順序 :
2
N2 の軌道順序 :
2 u,
[1
u,
[1 u,
3
u,
3 g] - O2 の場合と逆転
g] - O2 の場合と逆転
<N2 の分子軌道>
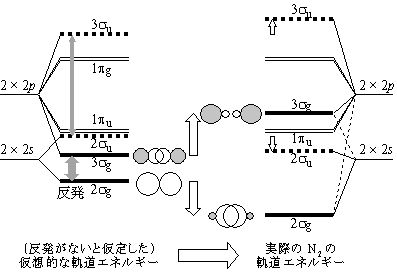
 2
2 g-3
g-3 g
(2
g
(2 u-3
u-3 u)
近づく
u)
近づく  反発
反発| 電子配置 : | [1 g2,
1 g2,
1 u2] u2] |
2 g2 g2 |
2 u2 u2 |
1 u4 u4 |
3 g2 g2 |
| [内殻] | 結合性 | 反結合性 | 結合性 | 結合性 | |
| (右のようにとることもある) | (非結合性) | (非結合性) |
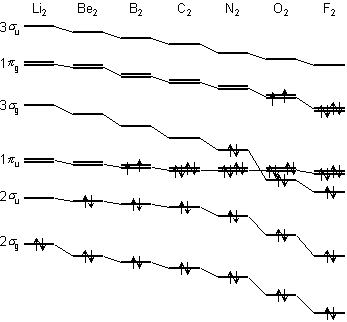
<第2周期元素 X2 分子の MO>
 ) ...
s-p 分裂大 (s
) ...
s-p 分裂大 (s  内殻的)
内殻的)
 N2 間で
[1
N2 間で
[1 u,
3
u,
3 g] 逆転
g] 逆転
 v)
v)
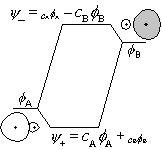
 相互作用-小
相互作用-小
 局在性が高い
局在性が高い
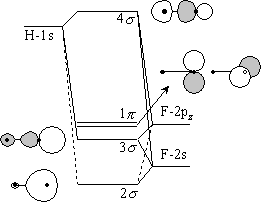
6.4.1 HF の分子軌道
| 1s(H) | 2s(F) | 2p(F) | ||
4 |
1.05 | -0.52 | 0.82 | 反結合性 |
1 |
1.00 | 非結合性* | ||
3 |
-0.53 | 0.41 | 0.70 | 非結合性* |
2 |
0.15 | 0.95 | -0.08 | 結合性 |
結合次数 = 1
cf.) 2 -非結合性,
3
-非結合性,
3 -結合性 とすることもある。
-結合性 とすることもある。