で符号
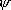 -
=
-
=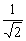 (
(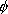 A -
A -
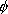 B)
B)

反結合性
 u
uungerade(独)
=odd(英)
(奇関数)
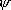 +
=
+
=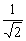 (
(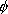 A +
A +
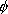 B)
B)

結合性
 g
ggerade(独)
=even(英)
(偶関数)
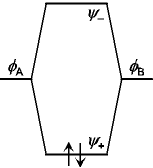
| 反転 i で符号 | |||
 -
= -
= ( ( A - A -
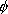 B) B)
|  反結合性 |  u uungerade(独) =odd(英) | 変わる (奇関数) |
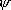 +
= +
=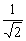 ( (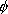 A + A +
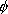 B) B)
|  結合性 |  g ggerade(独) =even(英) | 変わらない (偶関数) |
| side view | head view | C v v対称種 | D h h対称種 | 慣用名 *=反結合性 |
[ 軌道] 軌道]
| ||||

| 
| 
|  g g
| s-s 
|

| 
| 
|  u u
| s-s  * *
|
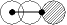
| 
| 
| s-p 
| |

| 
| 
|  g g
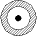
| p-p 
|

| 
| 
|  u u
| p-p  * *
|
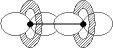
| 
| 
|  g g
| d-d 
|
[ 軌道] 軌道]
| ||||
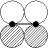
| 
| 
|  u u
| p-p 
|
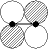
| 
| 
|  g g
| p-p  * *
|
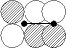
| 
| 
| p-d 
| |
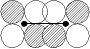
| 
| 
|  u u
| d-d 
|
[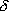 軌道] 軌道]
| ||||
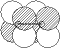
| 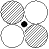
| 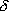
|  g g
| d-d 
|
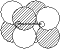
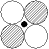
| 
| 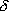
| 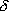 u u
| d-d 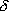 * *
|
 軌道 軌道
|  軌道 軌道
| 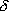 軌道 軌道
| |
| 分子軸を含む節面数 | 0 | 1 | 2 |
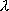 (l の分子軸への射影)
(l の分子軸への射影) | 0 | 1 | 2 |
| エネルギー | 低 |  | 高 |
 ,
,
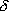 軌道では結合性軌道が gerade
軌道では結合性軌道が gerade

 軌道では
反結合性軌道が gerade
軌道では
反結合性軌道が gerade
<高次結合>
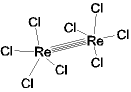
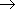 四重結合
四重結合
 ,
2
,
2  (d-d)
(d-d) ,
(d-d)
,
(d-d)
 g2
g2
 u4
u4
 g2
g2
 h)
h)
6.3.1 O2の分子軌道 (MO)
| 原子軌道 | 結合性 | 反結合性 | |
| 1s-1s | 1 g g
| 1 u u | 内殻軌道 |
| 2s-2s | 2 g g
| 2 u u | 内殻的 |
| 2pz-2pz | 3 g g
| 3 u u
|  に比べて に比べて
重なり大-分裂大 |
| 2px-2px | 1 u(x) u(x)
| 1 g(x) g(x)
| pz- に比べて に比べて
分裂小 2 重縮退 |
| 2py-2py | 1 u(y) u(y)
| 1 g(y) g(y)
|
電子配置 :
1 g2
1
g2
1 u2
2
u2
2 g2
2
g2
2 u2
3
u2
3 g2
1
g2
1 u4
1
u4
1 g2
g2
<結合次数>
<常磁性>
フントの規則 : 縮退軌道では電子はスピンが高くなる配置をとる
[解釈] 交換エネルギー安定化 or 電子間反発
O2 の電子基底状態は三重項
[1 g
(x)1
1
g
(x)1
1 g
(y)1] (常磁性)
g
(y)1] (常磁性)
| S (スピン量子数) | 2S + 1 (スピン多重度) | ||
| 一重項 | 0 | 1 | |
| 三重項 | (1/2 + 1/2 =) 1 | 3 | 常磁性 |
6.3.2 N2 の MO
<光電子スペクトル>
 - I.E.(MO)
- I.E.(MO)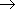 軌道エネルギーの測定
軌道エネルギーの測定
 u,
[1
u,
[1 u,
3
u,
3 g]
g]
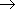 O2 の場合と逆転
[FAQ]
O2 の場合と逆転
[FAQ]
<N2 の分子軌道>
2s-2p 近づく  2
2 g-3
g-3 g
(2
g
(2 u-3
u-3 u) 近づく
u) 近づく
 反発
反発
・対称性の同じ軌道は反発する
電子配置 :
[1 g2
1
g2
1 u2]
(内殻),
2
u2]
(内殻),
2 g2
(結合性),
2
g2
(結合性),
2 u2
(非結合性),
1
u2
(非結合性),
1 u4
(結合性),
3
u4
(結合性),
3 g2
(非結合性)
[FAQ]
g2
(非結合性)
[FAQ]
結合次数 = 3
<第2周期元素 X2 分子の MO>
 ) ...
s-p 分裂
) ...
s-p 分裂 (s
(s 内殻的)
内殻的)
 N2 で
1
N2 で
1 u,
3
u,
3 g 逆転
g 逆転
 v)
v)
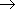 相互作用が小さい
相互作用が小さい 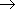 局在性が高い
局在性が高い
6.4.1 HF の分子軌道
2
| 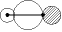
| [1s(H)] - 2pz(F) + 2s(F) 結合性 |
3
| 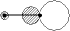
| [1s(H)] + 2pz(F) + 2s(F) 非結合性 |
1
| 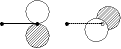
| 2px(F), 2py(F)
(二重縮退) 非結合性 (lp [lone pair; 孤立電子対] 軌道) |
4
| 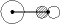
| 1s(H) + [2pz(F)] - [2s(F)] 反結合性 |