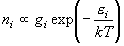 (6.1)
(6.1)
7.1 化学平衡
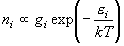 (6.1)
(6.1)
ex.) CO 分子
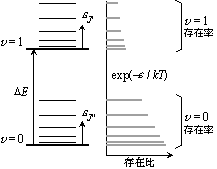 |
| 図 7.1 CO の振動回転準位分布 |
 = 1 (振動励起状態) の
= 1 (振動励起状態) の
 = 0 (振動基底状態) 対する存在比
= 0 (振動基底状態) 対する存在比
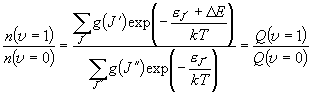
 状態を区別しない場合の存在確率
= 各状態の存在確率の和
状態を区別しない場合の存在確率
= 各状態の存在確率の和
 分配関数
分配関数
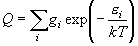
 = 1, 0 それぞれの最低回転エネルギーを
基点とした回転分配関数; Q'rot ,
Q"rot を使うと
= 1, 0 それぞれの最低回転エネルギーを
基点とした回転分配関数; Q'rot ,
Q"rot を使うと
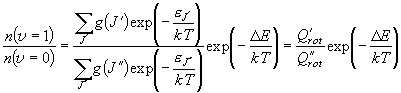
[化学平衡定数]
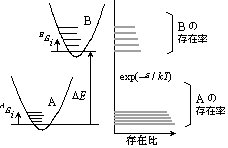 |
| 図 7.2 分子内準位分布と化学平衡 |
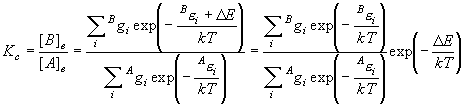
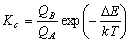 (7.1)
(7.1)
 平衡定数 (平衡状態の存在比)
= 分配関数の比
平衡定数 (平衡状態の存在比)
= 分配関数の比
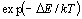 ... エネルギー基準点の違いによる
... エネルギー基準点の違いによる
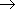 分子全体の分配関数
分子全体の分配関数
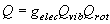 (7.2)
(7.2)
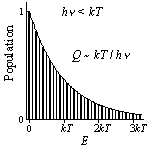 |
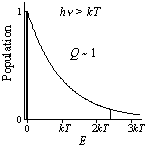 |
| 図 7.3 振動分配関数 |
7.2 振動分配関数
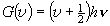 ,
,
 = 0, 1, 2, ... (2.5)
= 0, 1, 2, ... (2.5)
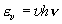 ,
,
 = 0, 1, 2, ... (7.3)
= 0, 1, 2, ... (7.3)
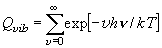 ... 等比級数
... 等比級数
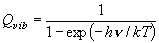 (7.4)
(7.4)
 分配関数 〜
温度 T における、実効的な状態の数
分配関数 〜
温度 T における、実効的な状態の数
7.3 回転分配関数
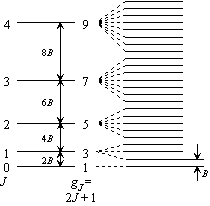 |
| 図 7.4 二次元回転の状態密度 〜 1 / B |
[直線分子]
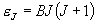 , J = 0, 1, 2,
... (3.3)
, J = 0, 1, 2,
... (3.3)
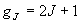 (3.5)
(3.5)
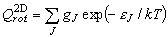
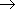 積分
積分
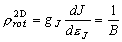
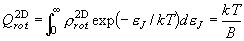 (7.5)
(7.5)
[非直線分子]
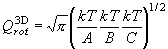 (7.6)
(7.6)
問題 7.1
C2 分子の基底状態 X 1g+ (gelec = 1,
= 1828 cm-1, B = 1.811 cm-1) と励起状態 a 3
u (gelec = 6,
= 1618 cm-1, B = 1.624 cm-1,
E = 716.2 cm-1) の 298 K, 1000 K における平衡定数を求めよ。
7.4 並進分配関数
[一次元並進]
・長さ l の一次元箱中の分子 (質量 m ) の並進運動
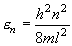 ,
n = 1, 2, 3, ... (7.7)
,
n = 1, 2, 3, ... (7.7)
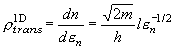
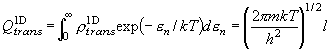 (7.8)
(7.8)
[三次元並進]
・lx  ly
ly  ly の箱中の並進運動
ly の箱中の並進運動
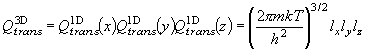 (7.9)
(7.9)
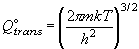 (7.10)
(7.10)
[相対並進(三次元)]
・m 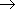
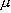 (換算質量)
(換算質量)
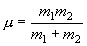 (2.3)
(2.3)
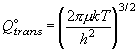 (7.11)
(7.11)
* 分配関数は一般に無次元だが、単位体積あたりの並進分配関数
(7.10, 7.11 式) は [体積]-1 の次元 (例えば m-3)
を持つ。 これは濃度 (単位は例えば molecules m-3)
の次元を持つことを意味している。
これは、例えば分解反応 AB 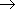 A + B の平衡定数,
A + B の平衡定数,
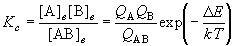 ,
が濃度の次元を持たなければならないことと対応している。
,
が濃度の次元を持たなければならないことと対応している。