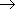 TS*
TS* 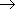 B の反応速度定数は、 遷移状態理論によれば、
B の反応速度定数は、 遷移状態理論によれば、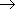 HNC)
HNC) 遷移状態 TS* を経由して進行する反応 A 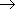 TS*
TS* 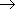 B の反応速度定数は、 遷移状態理論によれば、
B の反応速度定数は、 遷移状態理論によれば、
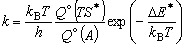 (5-1)
(5-1)
で与えられる。 ここで Q 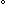 (A),
Q
(A),
Q 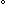 (TS*) は A, TS* の (単位体積あたりの)
分配関数、
(TS*) は A, TS* の (単位体積あたりの)
分配関数、  E *
は遷移状態と反応物のエネルギー差 (TS* の A を基準にしたエネルギー)
である。 この式は平衡定数の式 [演習問題 2] と類似している。
E *
は遷移状態と反応物のエネルギー差 (TS* の A を基準にしたエネルギー)
である。 この式は平衡定数の式 [演習問題 2] と類似している。
今ここでは、 HCN 分子の異性化反応
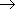 HNC (R3)
HNC (R3)
を考えることにすると、 平衡定数の評価の場合 [演習問題 4] と同様に、 (5-1) 式中の分配関数の比の部分は、 振動と回転の分配関数のみで書き表される。
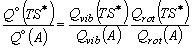 (5-2)
(5-2)
振動分配関数は、 演習問題 4 と同様に、 次式で評価される。
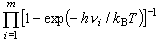 (5-3)
(5-3)
|
[問題 5-1] HCN は4つの振動自由度を持ち、 振動の波数は 794, 794, 2177, 3286 (cm-1) である。 遷移状態は2つの振動自由度を持ち振動波数は 1999, 2554 (cm-1) である。 1000 K および 3000 K における、 振動分配関数の比 Qvib (TS*) / Qvib (HCN) を計算せよ。 |
HCN 直線分子の分配関数は、 演習問題 4 と同様に、 次式で評価される。
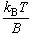 (B : 回転定数)
(5-4)
(B : 回転定数)
(5-4)
波数単位で与えられている回転定数を B' とすると、 B = hc 0 B' となるので、
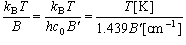 (5-4')
(5-4')
となる。
遷移状態 TS* は三角形の構造をとるため、
3次元の回転自由度を持つ。
非直線分子の回転分配関数は、 直線分子の場合と同様、
和を積分に置き換えることで、 次式で近似される。
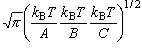 (5-5)
(5-5)
ここで、 A, B, C は3つの回転主軸の周りの回転定数である。 上と同様に、 波数単位で与えられている回転定数を、 A', B', C' とすると、
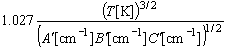 (5-5')
(5-5')
|
[問題 5-2] HCN は直線分子であり、 回転定数は 1.534 [cm-1] である。 遷移状態 TS* は非直線分子であり、 3つの回転定数は、 13.92, 1.875, 1.652 [cm-1] である。 1000 K および 3000 K における、回転分配関数の比 Qrot (TS*) / Qrot (HCN) を計算せよ。 TS* のエネルギーは HCN よりも、187.9 kJ mol-1 高い。 1000 K および 3000 K における、 反応 (2) の反応速度定数 [単位 : s-1] を求めよ。 |
一般に、 正方向の反応速度定数 kf と逆反応の反応速度定数 kr は平衡定数 KC と、
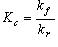 (5-6)
(5-6)
の関係がある。
|
[問題 5-3] 遷移状態理論による反応速度定数の式と、 演習問題 4 の平衡定数の式は、 (5-6) 式と矛盾しないことを示せ。 また演習問題 4 で求めた平衡定数を使って、 1000 K および 3000 K における、 逆反応 HNC  HCN (R-3)
の反応速度定数 [単位 : s-1] を計算せよ。 HCN (R-3)
の反応速度定数 [単位 : s-1] を計算せよ。
|