 B の濃度平衡定数は、
B の濃度平衡定数は、 HNC)
HNC) 反応 A  B の濃度平衡定数は、
B の濃度平衡定数は、
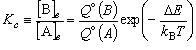 (4-1)
(4-1)
で与えられる。 ここで [A]e , [B]e
は平衡における A, B の濃度、
Q 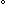 (A),
Q
(A),
Q 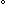 (B) は A, B の
(単位体積あたりの)
分配関数、
(B) は A, B の
(単位体積あたりの)
分配関数、 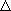 E
は反応のエネルギー差 (B の A を基準にしたエネルギー) である。
E
は反応のエネルギー差 (B の A を基準にしたエネルギー) である。
分子の(単位体積あたりの)分配関数は、
分子のすべての運動の分配関数の積で表わされる。
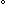 =
Q
=
Q  trans
Qelec Qvib Qrot
(4-2)
trans
Qelec Qvib Qrot
(4-2)
Q  trans,
Qelec, Qvib,
Qrot はそれぞれ、並進運動の (単位体積あたりの)
分配関数、 電子状態の分配関数、 振動分配関数、 回転分配関数である。
trans,
Qelec, Qvib,
Qrot はそれぞれ、並進運動の (単位体積あたりの)
分配関数、 電子状態の分配関数、 振動分配関数、 回転分配関数である。
今ここでは、HCN 分子の異性化反応
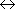 HNC (R3)
HNC (R3)
を考えることにする。 HCN も HNC も一重項の分子であり、 電子状態の分配関数はいづれも1である。 並進の分配関数は質量のみに依存し、 両者の質量は等しいので、 考えなくてよい。 したがって、(4-1) 式中の分配関数の比の部分は、 振動と回転の分配関数のみで書き表される。
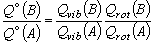 (4-3)
(4-3)
分配関数は、 分子の個々の状態の多重度をボルツマン因子を掛けて 足しあわせたものである。
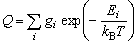 (gi : 状態 i の多重度,
Ei : 状態 i のエネルギー)
(4-4)
(gi : 状態 i の多重度,
Ei : 状態 i のエネルギー)
(4-4)
振動の分配関数は、 振動自由度が1つしかない2原子分子では、
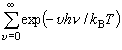 (4-5)
(4-5)
となる。
|
[問題 4-1] (4-5) 式の和が等比級数であることから、 次式を導け。
|
m 個の振動自由度がある多原子分子では、 (4-5')
式を個々の振動の振動数  i
について計算して、 掛け合わせたものになる。
i
について計算して、 掛け合わせたものになる。
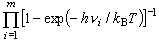 (4-6)
(4-6)
|
[問題 4-2] HCN と HNC はいづれも4つの振動自由度を持ち、 振動の波数は HCN が 794, 794, 2177, 3286 (cm-1)、 HNC が 484, 484, 2062, 3655 (cm-1) である。 1000 K および 3000 K における、 振動分配関数の比 Qvib (HNC) / Qvib (HCN) を計算せよ。 次式を用いると計算が効率的になる。 |
直線分子は2次元の回転の自由度を持ち、 (4-4) 式の和を積分に置き換えることで、 次の式で近似できる。
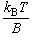 (B : 回転定数)
(4-7)
(B : 回転定数)
(4-7)
|
[問題 4-3] HCN と HNC はいづれも直線分子であり、 その回転定数は、それぞれ 1.534 (HCN)、 1.555 (HNC) [cm-1] である。 回転分配関数の比 Qrot (HNC) / Qrot (HCN) を計算せよ。 HNC のエネルギーは HCN よりも、49.8 kJ mol-1 高い。 1000 K および 3000 K における、HCN と HNC の平衡定数、 KC = [HNC]e / [HCN]e を求めよ。 |