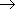 NaCl
(R1)
NaCl
(R1)
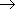 NaCl + Cl
(R2)
NaCl + Cl
(R2)
以下の反応、
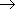 NaCl
(R1)
NaCl
(R1)
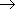 NaCl + Cl
(R2)
NaCl + Cl
(R2)
は「もりうち機構」で進行する。 その概要を反応 (R1) の場合について図 1-1 に示す。
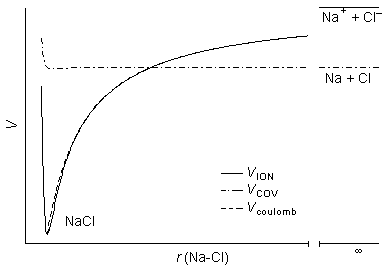 |
| 図 1-1. もりうち機構 (Harpoon Mechanism) |
共有結合性ポテンシャル (VCOV ) 上で Na と Cl を近づけると、 イオン結合性ポテンシャル (VION ) との交差点から先では VION の方が安定であるために、 ここからは VION 上を近づいていく。 交差点では Na が Cl に電子の「もり」を撃って Na+ と Cl- になり、静電力によって Cl- を引き寄せることから「もりうち機構」と呼ばれる。 Na と Cl がこの交差点以下の距離に近づけば反応がおこる。 単純なモデルでは、VCOV は一定、すなわち、
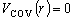 (1-1)
(1-1)
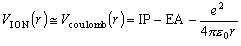 (1-2)
(1-2)
 0 は真空の誘電率、
e は電子の電荷である。
0 は真空の誘電率、
e は電子の電荷である。|
[問題 1-1] イオン結合性ポテンシャルと共有結合性ポテンシャルの 交差点における距離 rc の式を書け。 また、IP(Na) = 5.14 eV, EA(Cl) = 3.61 eV, EA(Cl2) = 2.54 eV を用いて、反応 (R1) および (R2) の場合の rc の値 [単位 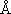 ] を求めよ。 ] を求めよ。*(注1) "eV" (エレクトロンボルト/電子ボルト) は電子1個を 1 V の電位差に逆らって移動するのに必要なエネルギーである (V = J C-1 である)。 |
(R1) の反応速度は、 Na と Cl が距離 rc 以下に近づくような衝突が起こる頻度である。 今、 Na と Cl の相対並進運動を考えると、 反応性の衝突が起こる頻度 (反応速度) は、反応断面積、
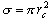 (1-3)
(1-3)
を持つ Na 原子が、 相対速度  で単位時間あたりに掃引する体積中にある Cl 原子の数である。
で単位時間あたりに掃引する体積中にある Cl 原子の数である。
 (Cl 濃度) (1-4)
(Cl 濃度) (1-4)
反応速度定数 k は、R を Cl 濃度で割ったものであるから、
である。絶対温度 T における平均相対並進速度は、 マクスウェル−ボルツマン速度分布から、
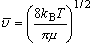 (1-6)
(1-6)
となる。 ここで、k B はボルツマン定数、
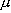 は2個の粒子の換算質量、
は2個の粒子の換算質量、
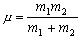 (m 1, m 2 : 各粒子の質量)
(1-7)
(m 1, m 2 : 各粒子の質量)
(1-7)
である。
|
[問題 1-2] (1-5) 式の反応速度定数を、rc ,  , T
から評価する式を書け。
また (R1), (R2) の反応の、 反応断面積 [単位 : , T
から評価する式を書け。
また (R1), (R2) の反応の、 反応断面積 [単位 :
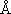 2]、 298 K における反応速度定数
[単位 : cm3 molecule-1 s-1
(cm3 s-1)] を計算せよ。
原子の質量は、 m (Na) = 23.0 amu, m (Cl) = 35.0 amu
を用いよ。また
(R2) の反応速度定数の実測値 (298 K)、 6.7 2]、 298 K における反応速度定数
[単位 : cm3 molecule-1 s-1
(cm3 s-1)] を計算せよ。
原子の質量は、 m (Na) = 23.0 amu, m (Cl) = 35.0 amu
を用いよ。また
(R2) の反応速度定数の実測値 (298 K)、 6.7  10-10 cm3 s-1 と計算値を比較せよ。
10-10 cm3 s-1 と計算値を比較せよ。*(注1) 'amu' (atomic mass unit / 原子質量単位) は 12C の原子核の質量の 1/12 と定義される。アボガドロ数 NA は、 1モルの 12C の質量が正確に 12 g となるように定義されている。 *(注2) 反応 (R2) の生成物は NaCl + Cl であるが、Na+ と Cl2- の引力部分のみが反応速度を決定しているため、 Na + Cl 同様に、入口部分の「もりうち機構」を考えるだけよい。 |