 |
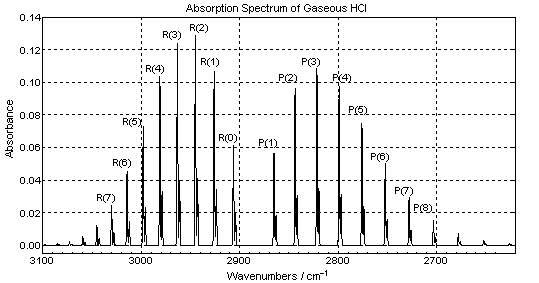
| 図 3-1. HCl の赤外吸収スペクトル |
上の図は気体 HCl 分子の赤外吸収スペクトルである。この吸収は HCl
分子の振動遷移 (振動量子数  = 1
= 1
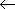 0) に対応するが、HCl
分子の回転状態による分裂が見られる。
回転速度によって、原子間距離が変化しないという近似 (剛体回転子近似)
のもとでの回転運動の量子力学による解は以下のようになる。
0) に対応するが、HCl
分子の回転状態による分裂が見られる。
回転速度によって、原子間距離が変化しないという近似 (剛体回転子近似)
のもとでの回転運動の量子力学による解は以下のようになる。
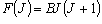 ( J : 回転量子数 = 0, 1, 2, ...) (3-1)
( J : 回転量子数 = 0, 1, 2, ...) (3-1)
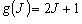 (3-2)
(3-2)
ここで回転定数 B は、エネルギーあるいは波数単位で書くと、
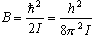 (エネルギー単位),
(エネルギー単位),
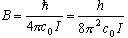 (波数単位)
(3-3)
(波数単位)
(3-3)
となる。 I は慣性モーメントであり、2原子分子では
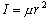 (
(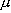 : 換算質量、r : 核間距離)
(3-4)
: 換算質量、r : 核間距離)
(3-4)
となる。 P(J ) と書かれた吸収線 (P 枝) は振動基底状態
( = 0) の回転量子数 J の状態から、
振動励起状態 (
= 0) の回転量子数 J の状態から、
振動励起状態 ( = 1) の回転量子数が
J - 1 の状態への吸収であり、
R(J ) と書かれた吸収線 (R 枝) は、振動基底状態の
J から、 振動励起状態の J + 1
への吸収である。
= 1) の回転量子数が
J - 1 の状態への吸収であり、
R(J ) と書かれた吸収線 (R 枝) は、振動基底状態の
J から、 振動励起状態の J + 1
への吸収である。
P 枝の回転線の強度, IP (J )
[または R 枝の回転線の強度, IR (J )] は、
吸収する状態の濃度、すなわち振動基底状態の回転状態の分布
(濃度) に比例する。絶対温度 T
における回転状態のボルツマン分布則から、
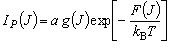 ,
または
,
または 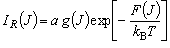 (3-5)
(3-5)
となる。ここで、k B はボルツマン定数, a は比例定数である。(3-5) 式を変形すると、
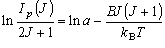 ,
または
,
または 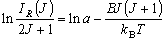 (3-6)
(3-6)
となる。従って、測定された回転線強度から計算された (3-6) 式の左辺を F (J ) に対してプロットすると、その傾きは - (1 / k BT ) を与える。 これをボルツマンプロットと呼ぶ。
|
[問題 1-3] P(J ) あるいは R(J ) の一連の回転線の強度の ボルツマンプロットから、この測定が行われた温度を推定せよ。 回転線の強度は表 3-1 の値を用いてよい。 回転定数には B = 10.4 cm-1 を用いよ。 |
*波数単位 cm-1 はエネルギーと線形な単位であるために、
分光学では波長よりも、好んで使用される。
またしばしばエネルギーの単位としても使われる。 振動数
 の光子1個のエネルギーは
h
の光子1個のエネルギーは
h  、 振動数
、 振動数
 と波数
と波数
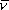 との関係は
との関係は
 =
c 0
=
c 0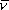 (c 0 は真空中の光速) である。
(c 0 は真空中の光速) である。
| Line | Position / cm-1 (H35Cl) |
Intensity (H35Cl) |
Position / cm-1 (H37Cl) |
|---|---|---|---|
| R7 | 3030.09 | 0.0267 | 3027.79 |
| R6 | 3014.42 | 0.0485 | 3012.13 |
| R5 | 2998.05 | 0.0779 | 2995.79 |
| R4 | 2981.00 | 0.1101 | 2978.76 |
| R3 | 2963.29 | 0.1349 | 2961.07 |
| R2 | 2944.91 | 0.1399 | 2942.72 |
| R1 | 2925.90 | 0.1166 | 2923.73 |
| R0 | 2906.25 | 0.0658 | 2904.11 |
| P1 | 2865.10 | 0.0617 | 2863.02 |
| P2 | 2843.63 | 0.1026 | 2841.58 |
| P3 | 2821.57 | 0.1156 | 2819.56 |
| P4 | 2798.94 | 0.1046 | 2796.97 |
| P5 | 2775.76 | 0.0802 | 2773.83 |
| P6 | 2752.04 | 0.0533 | 2750.14 |
| P7 | 2727.78 | 0.0312 | 2725.92 |
| P8 | 2703.01 | 0.0162 | 2701.19 |
*注 : 各回転線の横にある強度の小さいピークは H37Cl によるものである。 この問題ではこのピークは無視してよい。