Involves neither intermediate nor transition state
 0th order approximation
0th order approximationAssumption: statistically equal distribution in final states
Involves neither intermediate nor transition state
 0th order approximation
0th order approximation
cf.) Photodissociation of diatomic molecules (HCl, HI, etc.):
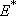 (excess energy)
(excess energy)
 distributes only in translation
distributes only in translation
| ex.) | Photodissociation of HCN at 215 nm (46512
 ) : ) : | |||
HCN + 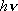 (46512 (46512
 ) ) |
 H + CN( H + CN( = 0)
+ 3211 = 0)
+ 3211  |
[channel-0] | ||
 H + CN( H + CN( = 1)
+ 1151 = 1)
+ 1151  |
[channel-1] | |||
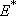  rel. translation + CN rotation
rel. translation + CN rotation | ||||
Probability of a specific rovibrational state

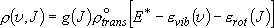 (3.1.1)
(3.1.1)
| ex.) | Rotational distribution of CN via channel-1
 | |
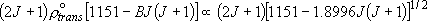 (
(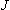 max = 24, fig. 3.1) max = 24, fig. 3.1) |
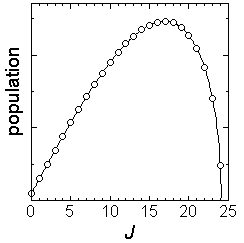
Fig. 3.1 Rotational distribution of CN formed via HCN +
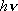 (channel-1)
(channel-1)
Probability of a specific vibrational state (indistinctive of
rotational states)  Rotational sum:
Rotational sum:
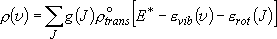 ,
,
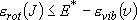 (3.1.2)
(3.1.2)
(summation  integration)
integration)
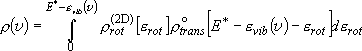
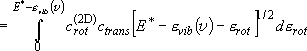
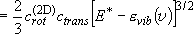 (3.1.3)
(3.1.3)
| ex.) | Branching ratio of channel-0 : channel-1 = (3211)3/2 :
(1151)3/2  4.66 : 1 4.66 : 1 |
|
Problem-3.1 [OPTION] Derive an equation similar to 3.1.3 for the case that an atom and a non-linear molecule (3-D rotation) are formed. |
[Rotational Sum]
Rotational sum for the case that two fragments are formed
(i.e., Branching probability for the specific vibrational state) :
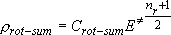 (3.1.4)
(3.1.4)
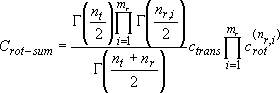 (3.1.5)
(3.1.5)
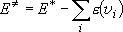 : Energy partitioned into
translation and rotation
(
: Energy partitioned into
translation and rotation
(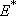 : Total excess energy)
: Total excess energy)
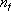 : Translational degree of
freedom (= 3),
: Translational degree of
freedom (= 3),
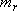 : Number of rotators,
: Number of rotators,
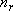 : Total rotational degree of
freedom (
: Total rotational degree of
freedom (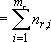 )
)
for integer  :
:
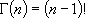 ,
,
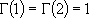
for half integer  :
:
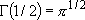 ,
,
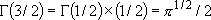 , ...
, ...
[Coefficients for rotational sum (eq. 3.1.5) for specific cases]
|
Problem-3.2 1) Calculate the prior vibrational energy distribution of OH formed via the reaction O( 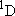 ) + H2 ) + H2
 OH + H
( OH + H
(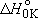 = -182.2 = -182.2
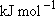 ) at 298 K.
Considering the thermal energy of the relative translation, ) at 298 K.
Considering the thermal energy of the relative translation,
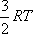 , and that of rotation, , and that of rotation,
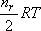 , (note that , (note that
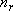 = 2 for H2),
the total excess energy at temperature = 2 for H2),
the total excess energy at temperature 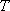 is; is;
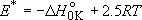 .
The vibrational frequency of OH is 3568 .
The vibrational frequency of OH is 3568  . .2) [OPTION] Calculate the prior rotational distribution OH in its vibrational ground state (  = 0) formed in the
above reaction.
The rotational constant of OH is 18.51 = 0) formed in the
above reaction.
The rotational constant of OH is 18.51  . .
|
Branching probability for a reaction channel 
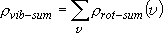 (vibrational sum)
(vibrational sum)
| ex.) | O( ) + HD ) + HD |
 H + OD H + OD | channel-a | ||
 D + OH D + OH |
channel-b | ||||
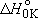 [O(
[O(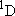 ) + H2 ) + H2  OH + H] = -182.2
OH + H] = -182.2 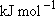 Vibrational frequencies (  ) -
OH: 3568, OD: 2632, H2: 4162, HD: 3633 ) -
OH: 3568, OD: 2632, H2: 4162, HD: 3633Rotational constants (  ) -
OH: 18.51, OD: 9.87 ) -
OH: 18.51, OD: 9.87(after ZPE & thermal corr. @ 298 K) 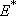 (a) =
15952, (a) =
15952, 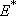 (b) = 15484
( (b) = 15484
( ) )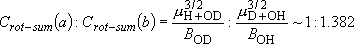  max(a) = 6
[15792 max(a) = 6
[15792  ], ],
 max(b) = 4
[14272 max(b) = 4
[14272  ] ] | |||||
Branching ratio =
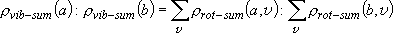
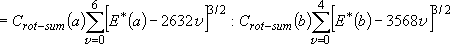 = 1 : 1.017 = 1 : 1.017 | |||||
| cf.) | summation  integration integration | |
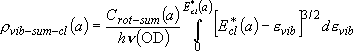
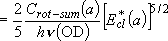 (3.2.1) (3.2.1)note) 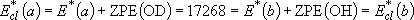 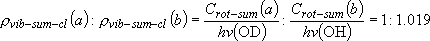 |
[Vibrational sum]
General formula by replacement of summation by integration :
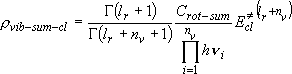 (3.2.2)
(3.2.2)
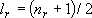 ,
,
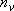 : vibrational degree of freedom,
: vibrational degree of freedom,
 i : vibrational frequency
i : vibrational frequency
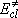 : excess energy
measured from the classical origin
: excess energy
measured from the classical origin
| ex.) | O(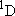 ) + CH4 ) + CH4
 OH + CH3
( OH + CH3
(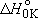 = -182.3 = -182.3
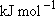 ) )- Prior vibrational distribution of OH (298 K) | ||
Motion other than OH-vibration  (3.2.2), (3.2.2),
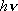 OH = 3568 OH = 3568
 ZPE(CH3) = 76.1 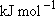
 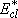 = (182.3 + 76.1) [
= (182.3 + 76.1) [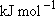 ] + 3RT = 22222 ] + 3RT = 22222
 cf.) 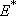 = 182.3
[ = 182.3
[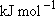 ] + 3 ] + 3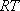 = 15860 = 15860
  max = 4
[14272 max = 4
[14272  ], ],
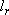 = (3 + 2 + 1) / 2 = 3, = (3 + 2 + 1) / 2 = 3,
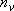 = 6, = 6,
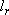 + +
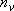 = 9 = 9Vibrational distribution  (fig. 3.2)
(fig. 3.2) = 0 1 = 0 1 = 1 0.207 = 1 0.207 = 2 0.0306 = 2 0.0306 = 3 0.00270 = 3 0.00270 = 4 9.60 = 4 9.60
 10-5 10-5 | |||
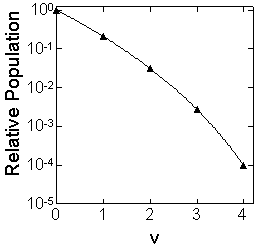
Fig. 3.2 Vibrational distribution of OH formed via
O(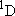 ) + CH4
) + CH4
|
Problem-3.3 Calculate the prior vibrational distribution of OH formed by O( 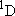 ) + C2H6 ) + C2H6
 OH + C2H5
( OH + C2H5
(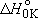 = -210.7 = -210.7
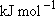 , ZPE(C2H5) = 148.5 , ZPE(C2H5) = 148.5
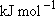 ) similarly to above, and compare it with
the cases for O( ) similarly to above, and compare it with
the cases for O(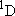 ) + H2 and
O( ) + H2 and
O(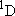 ) + CH4. ) + CH4.
|
[Atoms] (except for the excited states of rare gas atoms)
(spectrum) Term :
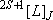
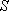 : electron spin q. n.
: electron spin q. n.
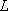 : electron orbital angular momentum
q. n.
: electron orbital angular momentum
q. n.
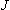 : total angular momentum q. n.
: total angular momentum q. n.
[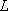 ] : symbolic representation of
] : symbolic representation of
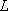 - S, P, D, F, G, H, ... for
- S, P, D, F, G, H, ... for
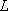 = 0, 1, 2, 3, 4, 5, ...
= 0, 1, 2, 3, 4, 5, ...
Total degeneracy : 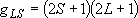
Degeneracy of the fine-structure state:
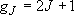
ex.)
| term |  |
 |
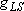 |
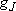 |
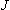 |
fine str. term |
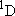 | 2 | 0 | 5 | 5 | 2 | |
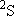 | 0 | 1/2 | 2 | 2 | 1/2 | |
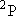 | 1 | 1/2 | 6 | 2 | 1/2 | 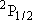 |
| 4 | 3/2 | 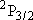 | ||||
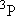 | 1 | 1 | 9 | 1 | 0 | 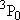 |
| 3 | 1 | 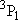 | ||||
| 5 | 2 | 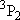 | ||||
| ex.) | branching ratio | ||||
HCl + 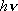 |
 H +
Cl( H +
Cl(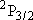 ) ) |
(a) | 4 
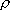 trans(a) trans(a) | ||
 H +
Cl( H +
Cl(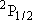 ) ) |
(b) | 2 
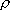 trans(b) trans(b) | |||
[Linear Molecules]
(spectrum) Term :
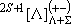
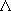 : projection of
: projection of
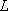 to the molecular axis
to the molecular axis
 : projection of
: projection of
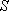 to the molecular axis
to the molecular axis
[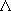 ]: symbolic representation of
]: symbolic representation of
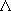 -
- 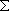 ,
,
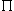 ,
, 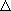 ,
,
 , ... (for
, ... (for 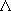 =
0, 1, 2, 3, ...)
=
0, 1, 2, 3, ...)
(+-): parity (+ or -, only for S states)
Total degeneracy : 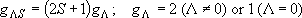
Degeneracy of the fine-structure state :
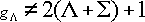
ex.)
| term |  |
 |
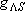 |
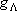 |
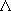 + +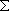
|
fine str. term |
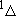 | 2 | 0 | 2 | 2 | 2 | |
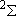 | 0 | 1/2 | 2 | 1 | 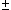 1/2 1/2 | |
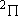 | 1 | 1/2 | 4 | 2 | 1/2 | 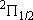 |
| 2 | 3/2 | 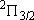 | ||||
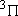 | 1 | 1 | 6 | 2 | 0 | 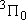 |
| 2 | 1 | 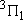 | ||||
| 2 | 2 | 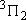 | ||||
| ex.) | branching ratio | ||||
| NH3 |  H2 +
NH( H2 +
NH(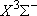 ) ) |
(X) | 3 
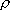 vib-sum(X) vib-sum(X) | ||
 H2 +
NH( H2 +
NH(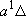 ) ) |
(a) | 2 
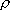 vib-sum(a) vib-sum(a) | |||
[Non-Linear Molecules]
(spectrum) Term :
 : symmetry species of the electronic
state ...
: symmetry species of the electronic
state ... 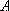 ,
, 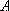 ',
',
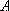 2,
2,
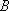 1,
1, 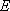 ,
,
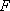 , etc.
, etc.
Total degeneracy : 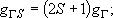
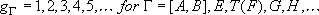
Degeneracy of the fine-structure state :
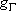
ex.)
| term | 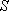 |
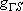 |
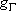 |
fine str. term |
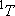 | 0 | 3 | 3 | |
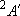 | 1/2 | 2 | 1 | |
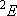 | 1/2 | 4 | 2 | 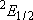 |
| 2 | 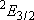 | |||
| ex.) | branching ratio | ||||
| CH3OH |  H +
CH3O( H +
CH3O(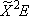 ) ) |
(X) | 4 
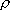 vib-sum(X) vib-sum(X) | ||
 H +
CH3O( H +
CH3O(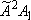 ) ) |
(A) | 2 
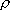 vib-sum(A) vib-sum(A) | |||
[Number of optical isomers]
| ex.) | branching ratio | ||||
CFCl2Br +
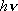 |
 Cl(
Cl(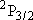 ) +
CFClBr ) +
CFClBr |
(a) | 2 
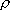 vib-sum(a) vib-sum(a) | ||
 Br(
Br(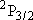 ) +
CFCl2 ) +
CFCl2 |
(b) | 2 
 vib-sum(b) vib-sum(b) | |||
channel-a  two optical isomers for CFClBr
(= two reaction pathway = inversion doubling)
two optical isomers for CFClBr
(= two reaction pathway = inversion doubling)
[Rotational distribution and nuclear spin statistics]
- Nuclear spin 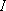 :
:
- Resultant total nuclear spin of a molecule
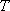 :
:
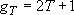
- Bose/Fermi particle-Bose/Fermi statistics
(symmetric/assymmetric to permutation)
| ex.) |
H2( = 0) -
Rotational state distribution = 0) -
Rotational state distribution- H nucleus :  = 1/2
(= proton / Fermi particle) = 1/2
(= proton / Fermi particle)
 tot should be
Asymmetric tot should be
Asymmetric- 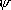 elec
( elec
(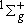 ) : Sym., ) : Sym.,
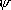 vib
( vib
( = 0) : Sym. = 0) : Sym. |
| ortho-H2 | para-H2 | ||
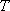 |
1 (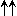 ) ) | 0 (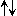 ) ) | |
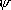 n.s n.s |
Sym. | 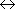 | Asym. |
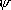 rot rot |
Asym. | 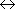 | Sym. |
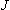 |
1, 3, ... (odd) | 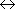 |
0, 2, ... (even) |
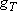 
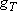 |
3  ( (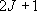 ) ) |
1  (
(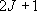 ) ) | |
| ex.) |
N2 or D2( = 0) -
Rotational state distribution = 0) -
Rotational state distribution- N or D nucleus : 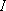 = 1
(Bose particle) = 1
(Bose particle)
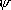 tot should be
Symmetric tot should be
Symmetric |
| ortho-N2/D2 | para-N2/D2 | ||
 |
0 ( ) or
2 ( ) or
2 (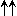 ) ) |
1 (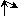 ) ) | |
 n.s n.s |
Sym. |  | Asym. |
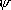 rot rot |
Sym. | 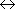 | Asym. |
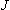 |
0, 2, ... (even) | 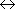 |
1, 3, ... (odd) |
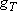 
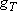 |
(1+5)  ( (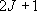 ) ) |
3  (
(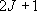 ) ) | |
- 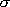 = 2
= 2 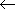 either in
sym. or asym. rotational state, rotational density of states is 1/2
either in
sym. or asym. rotational state, rotational density of states is 1/2
|
Problem-3.4 Calculate the prior branching fractions for the reaction of O( 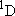 ) with CH4, ) with CH4,
1  = 11.96266 = 11.96266
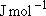 , , 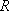 = 8.31451 = 8.31451
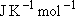
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||