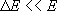 (microcanonical)
(microcanonical)
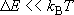 (canonical)
(canonical)
Classical Approximation / Limit
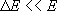 (microcanonical)
(microcanonical)
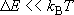 (canonical)
(canonical)
[1-D (One-Dimensional) Translation]
Motion of a particle (mass  ) in a 1-D box of
length
) in a 1-D box of
length 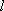 :
:
eigenvalue: 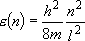 (
( = 1, 2, 3, ...) (2.1.1)
= 1, 2, 3, ...) (2.1.1)
density of states: 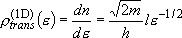 (2.1.2)
(2.1.2)
[3-D Translation]
Motion of a particle (mass  ) in a 3-D box
(
) in a 3-D box
(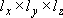 )
)
[Independent in  ,
,
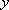 , and
, and
 directions]
directions]
eigenvalue: 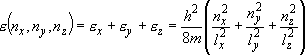 (
(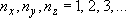 ) (2.1.3)
) (2.1.3)
density of states: 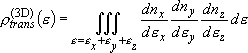
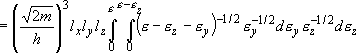
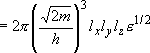 (2.1.4)
(2.1.4)
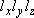 = volume:
= volume:
density of states per unit volume:
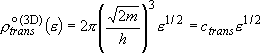 (2.1.5)
(2.1.5)
[3-D Relative Translation]
Relative translation of particle A and B:  (mass)
(mass) 
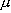 (reduced mass)
(reduced mass)
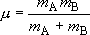 (2.1.6)
(2.1.6)
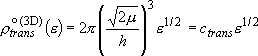 (2.1.7)
(2.1.7)
note:
1-D translation  activated complex in the
transition-state theory
activated complex in the
transition-state theory
2-D translation  diffusion on a surface of
an adsorbed molecule
diffusion on a surface of
an adsorbed molecule
3-D translation  reaction producing two
molecules
reaction producing two
molecules
|
Problem-2.1 1) Derive the expression for the density of states per unit area of 2-D translation. 2) Derive the 3-D translational energy distribution for canonical ensemble (Maxwell-Boltzmann distribution) at temperature T from equation (2.1.5). |
[Rotational Motion]
moment of inertia: 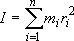 (2.2.1)
(2.2.1)
(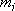 : mass of
: mass of
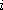 th atom,
th atom, 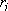 :
distance of
:
distance of 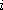 th atom from rotation axis)
th atom from rotation axis)
rotational constant: 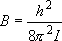 (2.2.2)
(2.2.2)
<Rotational symmetry number>
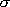 = number of indistinctive
rotational conformation
= number of indistinctive
rotational conformation
(same atoms are indistinctive)
ex.) 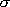 (N2)=2,
(N2)=2,
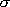 (HCl)=1,
(HCl)=1,
 (CO2)=2,
(CO2)=2,
 (H2O)=2,
(H2O)=2,
 (NH3)=3,
(NH3)=3,
 (C2H4)=4,
(C2H4)=4,
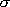 (CH4)=12
(CH4)=12
<Rigid rotor approximation>
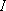 is constant (i.e.,
independent on the speed of rotation, the vibrational states, or etc.)
is constant (i.e.,
independent on the speed of rotation, the vibrational states, or etc.)
[1-D Rotator]
e.g. intramolecular rotations
[H3C-C C-CH3]
C-CH3]
eigenvalue: 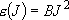 (
(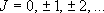 ), degeneracy:
), degeneracy:
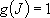 (2.2.3)
(2.2.3)
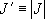

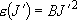 (
(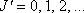 )
)
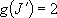 except for
except for
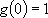 (2.2.4)
(2.2.4)
density of states: 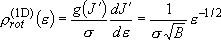 (2.2.5)
(2.2.5)
[2-D Rotator]
e.g. linear molecules [N2, CO2]
eigenvalue: 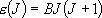 (
(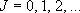 ),
degeneracy:
),
degeneracy: 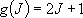 (2.2.6)
(2.2.6)
density of states: 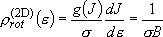 (2.2.7)
(2.2.7)
[3-D Rotator]
e.g. non-linear molecules
a) Spherical top ... 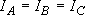 [CH4, SF6]:
[CH4, SF6]:
eigenvalue: 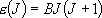 (
(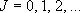 ),
degeneracy:
),
degeneracy: 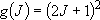 (2.2.8)
(2.2.8)
density of states: 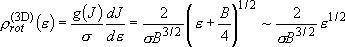 (2.2.9)
(2.2.9)
b) Symmetric top ... 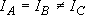 or
or
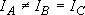 [NH3,
CH3]: (approximation)
[NH3,
CH3]: (approximation)
Asymmetric top ...
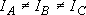 (H2CO, HCO):
(approximation)
(H2CO, HCO):
(approximation)
density of states: 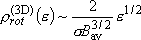 ,
,
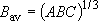 (2.2.10)
(2.2.10)
[Summary]
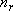
 rotational degree of freedom (dimension of rotation)
rotational degree of freedom (dimension of rotation)
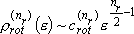 ,
,
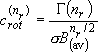 (2.2.11)
(2.2.11)
[Vibrational Motion]
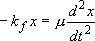 (
(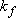 : force constant,
: force constant,
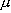 : reduced mass)
(2.3.1)
: reduced mass)
(2.3.1)
<Harmonic Oscillator Approximation>
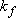 is constant
(i.e., independent of deviation
is constant
(i.e., independent of deviation  )
)
Solution to the classical mechanics:
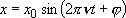 ,
,
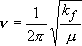 (
( : frequency [
: frequency [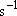 ])
(2.3.2)
])
(2.3.2)
[One Vibrator]
eigenvalue: 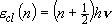 ,
,
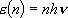 (2.3.3)
(2.3.3)
density of states: 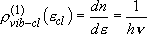 (2.3.4)
(2.3.4)
[ Vibrators]
Vibrators]
Number of vibrators: 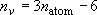 (non-linear molecule),
(non-linear molecule), 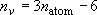 (linear molecule)
(linear molecule)
two vibrators: 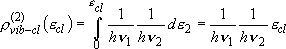
three vibrators: 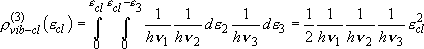
.....
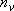 vibrators:
vibrators:
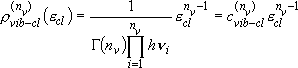 (2.3.5)
(2.3.5)
note:
1) Density of states is crude approximation (fig. 2.1) for vibration
since 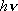
 200-3000
200-3000
 .
.
2) in eq. 2.3.5, 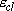 is the
energy from the classical origin (see fig. 2.2).
is the
energy from the classical origin (see fig. 2.2).
3) 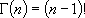 ,
,
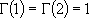
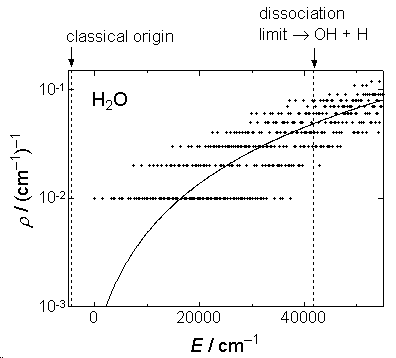
Fig. 2.1a Comparison of  by eq.
2.3.5 (solid line) and exact
by eq.
2.3.5 (solid line) and exact  (dots) for H2O.
(dots) for H2O.
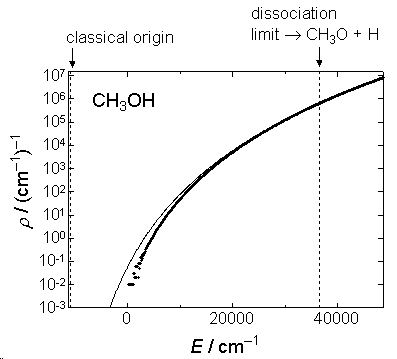
Fig. 2.1b Comparison of  by eq.
2.3.5 (solid line) and exact
by eq.
2.3.5 (solid line) and exact  (dots) for CH3OH.
(dots) for CH3OH.
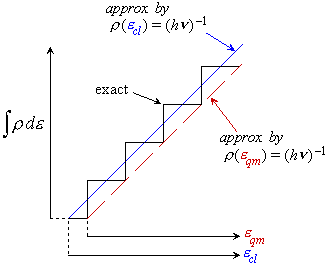
Fig. 2.2
|
Problem-2.2 Estimate the vibrational density of states for ethane [ 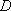 (C-C) = 377 (C-C) = 377 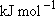 ]
at around dissociation threshold by eq. 2.3.5.
Use the following vibrational frequencies [Unit: ]
at around dissociation threshold by eq. 2.3.5.
Use the following vibrational frequencies [Unit:
 ; Values in parentheses are degeneracy of
the vibration.] ; Values in parentheses are degeneracy of
the vibration.]2954, 1388, 995, 289, 2896, 1379, 2969(2), 1468(2), 1190(2), 2985(2), 1469(2), 822(2) Note that the 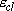 in eq. 2.3.5
is the energy from classical origin. in eq. 2.3.5
is the energy from classical origin.
|