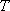 .
.
Canonical Ensemble
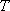 .
.
<Boltzmann Statistics>
Probability of finding a molecule in the state
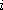 (of energy
(of energy
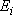 and multiplicity
and multiplicity
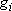 )
)
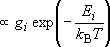
| ex.) | Distribution of the ground triplet states of atomic
oxygen; 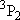 (
(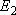  0, 0,
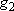 = 5), = 5),
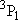 (
(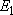 = 158.5 = 158.5
 , , 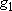 = 3), and
= 3), and 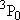 (
(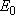 = 226.5 = 226.5
 , , 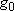 = 1); at 298 K (1
= 1); at 298 K (1  = 1.4388 K) = 1.4388 K) | |
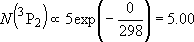 | ||
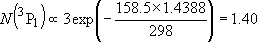 | ||
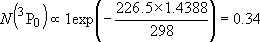 | ||
<Partition Function>
Probability of finding molecule A in the system
(e.g., A = HCN and not HNC, 1/2 H2 +
1/2 N2 + C, nor etc.) = Sum of the probability
of finding for all states of A 
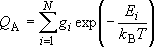 [partition function] (1.1.1)
[partition function] (1.1.1)
| ex.) | Distribution of the triplet ground states
(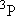 = = 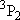 +
+ 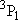 + +
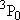 ) and the excited
( ) and the excited
(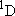 ) state
[ ) state
[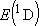 = 15867.7 = 15867.7
 , , 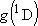 = 5] of atomic oxygen at 298 K:
= 5] of atomic oxygen at 298 K: | |
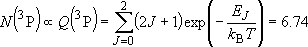 | ||
 | ||
| ex.) | Vibrational partition function of a harmonic oscillator
(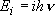 ): ): | |
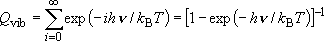 (1.1.2)
(1.1.2) | ||
<Chemical Equilibrium>
Ratio of the distributions of molecule B to A:
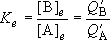 (When the same zero energy point was used to calculate both
(When the same zero energy point was used to calculate both
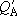 and
and
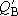 )
or
)
or
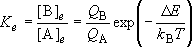 (1.1.3)
(When
(1.1.3)
(When 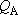 and
and
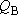 are calculated from an each
ground sate)
are calculated from an each
ground sate)
<Transition-State Theory>
Rate coefficient (A  [TS*]
[TS*]
 B)
B) 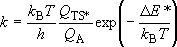 (1.1.4)
(1.1.4)
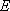 .
.
<Multiplicity>
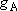 ) to that in the
state B (multiplicity
) to that in the
state B (multiplicity 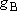 ; at the
same energy as A) =
; at the
same energy as A) = 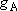 :
:
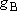
| ex.) | Atomic orbitals of H: 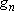 = =
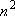 ( ( : principal q.n.), : principal q.n.),
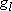 = = 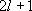 (
(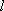 : azimuthal q.n.) : azimuthal q.n.) |
K-shell ( = 1):
1s ( = 1):
1s (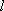 = 0, = 0,
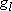 = 1) only = 1) only 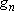 =
= 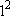 = 1 = 1 | |
L-shell ( = 2):
2s ( = 2):
2s (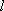 = 0, = 0,
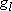 = 1),
2p ( = 1),
2p (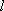 = 1, = 1,
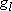 = 3) = 3)
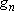 = =
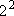 = 4 = 4 | |
M-shell ( = 3):
3s ( = 3):
3s (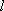 = 0, = 0,
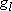 = 1),
3p ( = 1),
3p (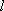 = 1, = 1,
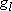 = 3),
3d ( = 3),
3d (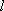 = 2, = 2,
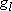 = 5) = 5) 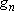 =
= 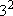 = 9 = 9 |
| ex.) | Electronic states of H-atom: | total multiplicity | |
| ground state: | 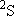 (
(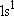 ) [ ) [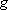 = =
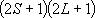 = 2 = 2
 1 = 2] 1 = 2] |
(K-shell) 2 | |
| excited states: | 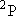 (
(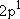 ) [ ) [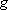 =
2 =
2  3 = 6] 3 = 6] |
(L-shell) 8 | |
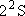 ( (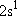 )
[ )
[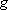 = 2 = 2  1 = 2] 1 = 2] | |||
| ex.) | Bending vibration (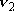 ) of
CO2 ... 2-D harmonic oscillator ) of
CO2 ... 2-D harmonic oscillator |
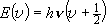 , ,
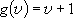 ;
( ;
( : vibrational q.n.) : vibrational q.n.) |
<Density of states>
 ]
]
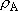 ) and B
(
) and B
(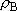 ) =
) =
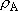 :
:
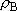
| ex.) | Photodecomposition of HCl at 248 nm (40320
 ): ): | ||
HCl + 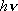 (40320
(40320  ) ) |
 H +
Cl( H +
Cl(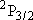 ) + ) +
 (4240 (4240
 ) ) | (a) | |
 H +
Cl( H +
Cl(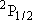 ) + ) +
 (3359 (3359
 ) ) | (b) | ||
Statistical branching ratio,
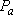 : :
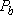 | |||
= 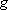 [Cl( [Cl(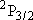 )] )]
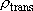 (4240 (4240
 ) : ) : 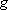 [Cl( [Cl(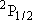 )] )]
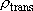 (3359 (3359
 ) ) | |||
=
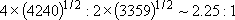 | |||
|
Problem-1 Calculate the statistical branching ratio between H + I( 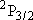 ) [channel-a] and H +
I( ) [channel-a] and H +
I(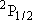 ) [channel-b] upon the
photolysis of HI at 266 nm.
Use the bond dissociation energy of HI [ ) [channel-b] upon the
photolysis of HI at 266 nm.
Use the bond dissociation energy of HI [  H + I(
H + I(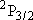 ) ] = 298 ) ] = 298
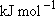 and excitation energy of
I( and excitation energy of
I(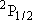 ) form
I( ) form
I(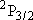 ) (ground state) =
0.943 eV. ) (ground state) =
0.943 eV.
|