The program expects following two input files in the current
directory.
| 1) | A GPOP-format file, basename.gpo. |
| 2) | A modification information file, basename.mod. |
The program
gpop1scf creates a template modification
file,
basename.mod
(or
basename_.mod). For example, if the sample
Gaussian output,
ethyl500.log, is processes, the newly
created modification template file,
ethyl500.mod
(or
ethyl500_.mod), looks like;
! gElec 2
! rotSymNbr 1
! numIsomers 1
! isTS false
! energyTST #
! setIntRotor idVib nSym moi1 moi2 V0 comment
Any characters from an exclamation mark '!' to the
end of the line are comments. The template file include typical
keys and value as comments.
The values for gElec (degeneracy of the
elctronic state), rotSymNbr (rotational symmetry number),
numIsomers (number of isomers), and isTS
(flag indicates transition state) are the default that are already set
in the GPOP-format file. Thus, if these values are correct, leave them
commented out, but if any value is wrong, remove '!' and
a white space follows, and type correct value. See below for the other
keys.
Valid Keys in .mod file
elState state_sym
Symmetry of the electronic state. It does not affect the rate constant
and thermodynamic calculation. It is rather important to give gElec
or eStates shown below, which are directly used for calculations.
default: determined from the output.
Degeneracy of the electronic state including both the electronic
spin degeneracy and the electronic angular momentum degeneracy.
For example for OH radical, one may need to specify to account for the
2Π electronic state (spin multiplicity = 2 and anglular momentum multiplicity = 2);
gElec 4
or specify the fine structures by
eStates (see below).
default: determined from the output (
note-1).
eStates nEstates (g energy)*nEstates
Fine elctronic states specification. If this key is specified,
the
gElec key is completely ignored.
nEstates is the number of electronic states,
followed by
nEstates pairs of
(g energy) where
g and
energy are the degeneracy and the energy (in
cm
–1 unit) of each state. Below is an example for
the OH radical with
2Π
3/2 and
2Π
1/2 spin-orbit states.
eStates 2 2 -69.6 2 69.6
pntGrp point_group
Point group of the molecule. It does not affect the rate constant
and thermodynamic calculation. It is rather important to give rotSymNbr
and numIsomers shown below, which are directly used for calculations.
default: determined from the output.
Rotational symmetry number. For example for
an H
2O molecule calculated with slightly asymmetric initial structure,
one may need to specify to correct for the symmetry number as;
rotSymNbr 2
default: determined from the output (
note-2).
Number of isomers. For example for a propene
(C
3H
6) moleclule calculated with slightly assymmetric initial
structure, one may need to specify to correct for the number of isomers as;
numIsomers 1
default: determined from the output (
note-3).
isomStates nIsomSts (n energy)*nIsomSts
Isomeric species specifications. If this key is specified, the
numIsomers key is ignored.
nIsomSts
is the number of isomeric species, followed by
nIsomSts
pairs of
(n energy) where
n and
energy are the number of occurrence and the energy
(in cm
–1 unit) of each isomeric species.
For example for butane (C
4H
10) with lowest
C2h (anti) conformer and two
enantiomers of
C2
(gauche) form, one may need to specify;
isomStates 2 1 0 2 247
A flag indicates the transition state. The value
flag must be either of 'true'
or 'false'.
default: determined from the output (
note-4).
energyTST energy
Energy (in hartree unit) for rate constant calculation,
and should correspond to the internal energy at 0 K. Since only the
differences (between reactants and transition states, etc.) are
significant, the energy can be defined from any zero point, which,
however, should be common for all relevant molecules or atoms.
useSCFenergy+ZPE
This key (without any value followed) tell the program to use
SCF level energy corrected for ZPE for rate constant calculations.
scaleFactVib factor
Change the vibrational-frequency scaling factor to
factor.
scaleFactZPE factor
This key tells the program to use, factor,
for the scaling of vibrational frequencies in the zero-point energy
calculation. This affects the results when used with
useSCFenergy+ZPE and/or setIntRotor.
setIntRotor
idVib nSym moi1 moi2 V0 comment
Definition of a intramolecular rotor.
idVib
is the index of the vibrational mode which is treated as a hindered
internal rotor. If this index is set to 0 or negative value,
gpop3tst automatically detects the most similar
vibrational mode (
note-5).
nSym is the symmetry number of the internal rotation.
moi1 and
moi2 inputs specifies
the intramolecular rotation and the format for these are the same as
that in
gpop6irt program.
V0 is the height of the hindrance potential.
if a positive
V0 input is found, the value is used
for calculation. If
V0 is zero, it is treated as
a free rotor. If
V0 is negative, V0 is calculated
from the eq. (2) below.
comment is an optional comment field.
The vibrational frequency is scaled by
scaleFactZPE
for the quantum mechanical correction and for the estimation of V0,
in order to keep the consistency of zero-point energy.
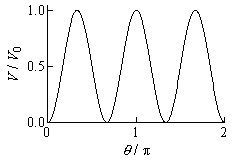
Intramolecular rotations
The intramolecular rotor specified by
setIntRotor
is treated as a sinusoidally hindered rotor with a potential energy
curve,
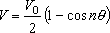
(1)
where
V0 is barrier height,
n is the
symmetry number of rotation (
nSym in
setIntRotor), and
θ is angle of rotation.
Its partition
function and thermodynamic functions are calculated by using
Pitzer-Gwin
approximation [
1] in the programs
tstrate and
gpop4thf.
The potential barrier height,
V0,
is estimated from
the harmonic frequency of corresponding vibrational mode,
ν,
as,
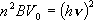
or
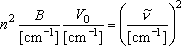
(2)
where
B is the reduced rotational constant of the rotor,
h is the Planck constant, and
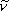
is the wavenumber
corresponding to the vibrational frequency.
The barrier height estimation by Eq. (2) is a fairly good
approximation for symmetric rotors with moderate barrier height,
such as methyl group (–CH
3).
Application of this method for asymmetric rotors may be even worse
than the harmonic oscillator approximation and must be done carefully.
BEx1D program
may be useful for precise analysis of asymmetric
rotors, though it requires a few more points of quantum chemical
calculations along the rotational coordinate.
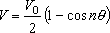 (1)
where V0 is barrier height, n is the
symmetry number of rotation (
(1)
where V0 is barrier height, n is the
symmetry number of rotation (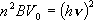
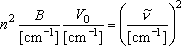 (2)
where B is the reduced rotational constant of the rotor,
h is the Planck constant, and
(2)
where B is the reduced rotational constant of the rotor,
h is the Planck constant, and
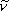 is the wavenumber
corresponding to the vibrational frequency.
The barrier height estimation by Eq. (2) is a fairly good
approximation for symmetric rotors with moderate barrier height,
such as methyl group (–CH3).
is the wavenumber
corresponding to the vibrational frequency.
The barrier height estimation by Eq. (2) is a fairly good
approximation for symmetric rotors with moderate barrier height,
such as methyl group (–CH3).