Moiety input
Each moiety if specified by a list of atoms. The first atom
in the list must be the pivot atom for intramolecular rotation.
The ordering of the indices is exactly the same as in the Gaussian
output. For example;
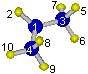 The pivot carbon atom[3] must be the first atom in the moiety-1 and
the counter pivot atom[1] must be the first atom in the moiety-2, while
the ordering of the other atoms in each moiety is arbitrary. Because
the counter moiety-2 usually contains all the other atoms that do not
belong to moiety-1, the moiety-2 may be specified with the abbreviation
mark '
The pivot carbon atom[3] must be the first atom in the moiety-1 and
the counter pivot atom[1] must be the first atom in the moiety-2, while
the ordering of the other atoms in each moiety is arbitrary. Because
the counter moiety-2 usually contains all the other atoms that do not
belong to moiety-1, the moiety-2 may be specified with the abbreviation
mark '
gpop6irt iprR100 3-5-6-7 1-2-4-8-9-10
specifies intramolecular rotation around C[3]-C[1] bond of the isopropyl
radical shown in the figure below.

@', such as;
gpop6irt iprR100 3-5-6-7 1-@
Each moiety input can only contain numeric letters
'0123456789' or hyphens '-', except that
moiety-2 may contain '@' as the second atom.