Following is the content of sample .mrt file, iprR100.mrt;

1:3-5-6-7
1:4-8-9-10

Each line corresponds to a internal rotor, with a format;

pivot-moi2:moi1

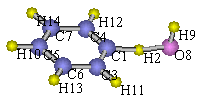
The moi1 input is the same as that in gpop6irt program, while the moiety-2 is specified by the pivot atom only. The sample input specifies the rotation around C[1]–C[3] bond and that around C[1]–C[4] bond.

  For the calculation of moment of inertia and rotational constant of bending vibrations, the following optional input is accepted. An example input is shown for the transition state of OH + benzene H-abstraction reaction.

1:2-8-9
z1:2-8-9
x1:2-8-9
y1:2-8-9

The first and the second lines are identical, and specifies a moiety consisting of H2, O8, and H9 rotating around C1-H2 axis.   Here, the z-axis is defined by the two pivot atoms, C1 and H2. The x-axis is defined so as it pass through the center of mass of the moiety, and y-axis perpendicular to both z- and x- axes.   The third line specifies the rotation around the axis parallel to x-axis and passing through the pivot, H2. In other words, this is a out of plane C1-H2-O8 bending (wagging).   Similarly, the fourth line specifies the rotation around the axis parallel to y-axis and passing through the pivot, H2, or the C1-H2-O8 in-plane bending (rocking).

  For more flexible specification of the rotation axis, following two types of the extension are also available.

v1:2-8-9|3-4
p1:2-8-9|3-7:4-6
i1:2-8-9|0:0:1

v-option:  The input beginning with 'v' specifies the rotation axis direction by the vector connecting two atoms specified after '|'. The first input line above specifies the rocking vibration of H2-O8-H9 moiety.
p-option:  The input beginning with 'p' specifies the rotation axis by two vectors. The second input line indicates the direction of the rotation axis is both perpendicular to C3-C7 and C4-C6 vectors, that is, it corresponds to the wagging vibarion of H2-O8-H9 moiety.   In this example, the second type of input with 'p' is necessary to specify the wagging vibration of the molecule deviated in the direction of wagging coordinates, because the deviation changes the center of mass of the moiety, and specification with 'x' is no longer the axis of wagging vibration.
i-option:  The 'i' option specifies the axes of rotation by cartesian vector in the input geometry. The third line in above example specifies the axis is cartesian (0,0,1) vector.

  The first part reports the single rotor properties as;

----- Uncoupled Properties -----
 ucR#1: I=  2.55110 B=  6.60799   1 (0.801)   2 (0.595)   8 (0.150)
 ucR#2: I=  2.55110 B=  6.60799   1 (0.801)   2 (0.595)   8 (0.150)

which are same as those reported by gpop6irt but in concise format.

  The second part reports the properties of coupled rotors as;

 DSYEV info:0  lw-opt:68.000
----- Coupling Calculation Results -----
 cpR#1: I=  2.02510 B=  8.32433 vec= -0.707  0.707
 cpR#2: I=  3.07709 B=  5.47843 vec=  0.707  0.707
----- Coupled - most resembling vibrations -----
 cpR#1:   2 (0.994)   8 (0.251)   3 (0.250) freq=128.193
 cpR#2:   1 (1.000)   7 (0.042)  20 (0.025) freq=115.293

The first line is a diagnostic message for DSYEV subroutine in LAPACK, which does not need to be care usually. The coupling calculation results show that the two input localized rotations couples with 1:1 ratio, and the resultant orthogonal roational coordinates and corresponding reduced moments of inertia are; where θ_i denotes the coordinate of i-th localized (input) rotation, ψ_j is the j-th orthogonal coordinates, and I_j is corresponding reduced moment of inertia. The most resembling vibrations output indicates that the poor similarity coefficients for input localized rotations are successfully improved by the appropriate coupling calculation, that is, the vibrational mode #2 with frequency 128.193 cm^–1 is assymetric internal rotation while mode #1 with frequency 115.293 cm^–1 is symmetric internal rotation.

  The last section reports the results of decoupling.

----- diagnostic of coupling -----
----- Decoupled Frequencies -----
 ucR#1: 120.578
 ucR#2: 120.578
----- Partition Function Correction Factor -----
 0.979

Decoupled frequencies are inversely calculated vibrational frequencies for uncoupled (localized) internal rotations. Because of the full symmetry of two local internal rotations, the results gave two identical frequencies for these two equivalent motion. The partition function correction factor must be used when calculating the partition function with localized approximation, and thus it is a measure of the strength of coupling.