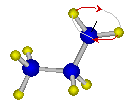
Fig. QS3-1. CH2 torsion of n-propyl radical.
Sample problem 2: nprCH2

bx1fitPlls input: nprCH2.fit
'#' is a title line:# n-propyl radical -.CH2 intramolecular rotation
outputOption FourierSerieswhich tells bx1fitPlls to generate input file for bx1HRsol named
'nprCH2.inp'. The program bx1HRsol requires
potential function in Fourier series.
optFuncs{
const
cos 2
cos 4
cos 6
cos 8
cos 10
cos 12
cos 14
cos 16
cos 18
}
tells bx1fitPlls that the regression function is:
y = a0
+ a1 cos(2x)
+ a2 cos(4x)
+ a3 cos(6x) + ...
+ a9 cos(18x).
xyTable{
0. 57.1562
deriv2 0. 283.094
0.414428431 69.7012
deriv1 0.414428431 0.
deriv2 0.414428431 -454.686
1.095630438 0.0000
deriv1 1.095630438 0.
deriv2 1.095630438 714.797
1.570796327 28.1917
deriv2 1.570796327 -580.236
}
Each line between block header 'xyTable{' and terminator '}'
defines a datum point. The two-column format datum line is
a regular datum point containing x (coordinate) and y
(potential energy), as explained in the previous step.
The three-columned line is a derivative datum.
deriv1, deriv2, etc. stand for first,
second, etc. derivative. The second column is x and third
is y', y", or etc., depending on the first column.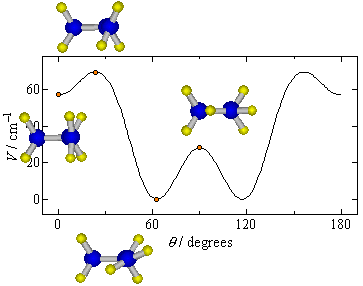
continue{
maxAbsQN 50 ! maximum absolute J
rotConst 10.575 ! cm-1
nuSpinSt 2 1 3 ! period = 2, alternation is 1,3,1,3,...
! symNumbr 2
!
output all
tempRange 200. 500. 50.
tempRange 600. 1200. 100.
tempRange 1400. 2000. 200.
tempRange 2500. 3000. 500.
tempList 298.
}
Any line in the block is copied to the bx1HRsol input,
'nprCH2.inp'.bx1fitPlls console output
Function: y = a0 + a1 * cos(2*x) + a2 * cos(4*x) + a3 * cos(6*x) + a4 * cos(8*x) + a5 * cos(10*x) + a6 * cos(12*x) + a7 * cos(14*x) + a8 * cos(16*x) + a9 * cos(18*x) y' = a1 * -2*sin(2*x) + a2 * -4*sin(4*x) + a3 * -6*sin(6*x) + a4 * -8*sin(8*x) + a5 * -10*sin(10*x) + a6 * -12*sin(12*x) + a7 * -14*sin(14*x) + a8 * -16*sin(16*x) + a9 * -18*sin(18*x) y" = a1 * -4*cos(2*x) + a2 * -16*cos(4*x) + a3 * -36*cos(6*x) + a4 * -64*cos(8*x) + a5 * -100*cos(10*x) + a6 * -144*cos(12*x) + a7 * -196*cos(14*x) + a8 * -256*cos(16*x) + a9 * -324*cos(18*x)The derived potential energy curve is shown in Fig. QS3-2 by a solid curve.
bx1HRsol input: nprCH2.inp
nprCH2.fit:# n-propyl radical -.CH2 intramolecular rotation
continue
block contents:maxAbsQN 50 ! maximum absolute J rotConst 10.575 ! cm-1 nuSpinSt 2 1 3 ! period = 2, alternation is 1,3,1,3,... ! symNumbr 2 ! output all tempRange 200. 500. 50. tempRange 600. 1200. 100. tempRange 1400. 2000. 200. tempRange 2500. 3000. 500. tempList 298.i) Here,
'maxAbsQN', the maximum absolute quantum number,
is set to 50. That is, the free rotor basis functions of
J = −50 to J = 50 (101 functions) are
used as expansion basis.'rotConst' sets the rotational constant
( = 'nuSpinSt' is nuclear spin
statistic information input. Here, for two indistinguishable
hydrogen atoms of CH2 rotor, the statistical weights for
even and odd J's are 1 and 3, respectively. Alternatively,
as shown in the next comment line, a key 'symNumber' can
be used to set the rotational symmetry number.output controls the output, as has been
described in the previous step. Here, all possible outputs
are generated by bex1HRsol.
potPars{ ! potential parameters
0 37.021012
2 31.151841
4 4.5381994
6 -17.268128
8 1.2278534
10 0.69347043
12 -0.23513126
14 -0.20930961
16 0.12201598
18 0.11437619
}
Each line in the block specifies the order ni and
coefficient ai for a term of Fourier.
Zero or positive order, ni ≥ 0, indicates
a cosine term, ai cos(ni x),
and negative order, ni < 0, indicates a sine
term, ai sin(|ni| x).
bx1HRsol output
'output all' is specified in the input,
bx1HRsol creates all possible output files for this example;
'nprCH2_eigen_values.csv' (eigen values),
'nprCH2_part_funcs.csv' (partition functions),
'nprCH2_eigen_vectors00.csv' (eigen vectors),
and 'nprCH2_eigen_funcs00.csv' (eigen functions).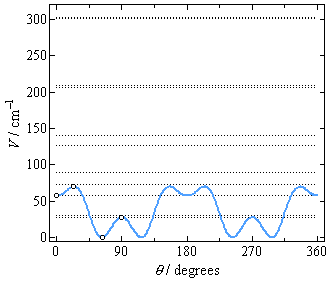
| eigen_values | 27.545063 | 29.921654 | 57.706454 | 72.501562 | 90.023541 | |||||
| eigen_vectors | (real) | (imag) | (real) | (imag) | (real) | (imag) | (real) | (imag) | (real) | (imag) |
| J(basis) | v0 | v1 | v1 | v2 | v2 | |||||
| ... | ... | ... | ... | ... | ... | |||||
| c(−5) | 0 | 0 | 0.0245 | 0 | −0.0298 | 0 | 0 | 0 | 0 | 0 |
| c(−4) | −0.0033 | 0 | 0 | 0 | 0 | 0 | 0.1270 | 0 | 0.0472 | 0 |
| c(−3) | 0 | 0 | 0.0812 | 0 | 0.1924 | 0 | 0 | 0 | 0 | 0 |
| c(−2) | −0.2680 | 0 | 0 | 0 | 0 | 0 | −0.6955 | 0 | −0.6529 | 0 |
| c(−1) | 0 | 0 | −0.7019 | 0 | −0.6797 | 0 | 0 | 0 | 0 | 0 |
| c(0) | 0.9248 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.3779 | 0 |
| c(1) | 0 | 0 | 0.7019 | 0 | −0.6797 | 0 | 0 | 0 | 0 | 0 |
| c(2) | −0.2680 | 0 | 0 | 0 | 0 | 0 | 0.6955 | 0 | −0.6529 | 0 |
| c(3) | 0 | 0 | −0.0812 | 0 | 0.1924 | 0 | 0 | 0 | 0 | 0 |
| c(4) | −0.0033 | 0 | 0 | 0 | 0 | 0 | −0.1270 | 0 | 0.0472 | 0 |
| c(5) | 0 | 0 | −0.0245 | 0 | −0.0298 | 0 | 0 | 0 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | |||||
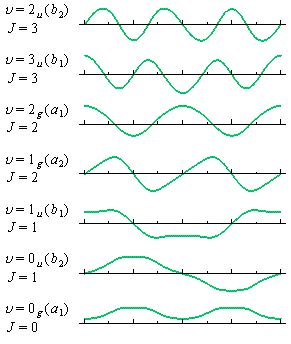
| eigen_ functions | (real) | (imag) | (real) | (imag) | (real) | (imag) | (real) | (imag) | (real) | (imag) |
| x | f0 | f1 | f1 | f2 | f2 | |||||
| 0 | 0.1670 | 0 | 0 | 0.0000 | −0.4193 | 0 | 0 | 0.0000 | −0.6448 | 0 |
| ... | ... | ... | ... | ... | ... | |||||
| 30 | 0.2471 | 0 | 0 | 0.2012 | −0.4416 | 0 | 0 | 0.3871 | −0.4215 | 0 |
| 60 | 0.4974 | 0 | 0 | 0.5115 | −0.4436 | 0 | 0 | 0.5767 | 0.0890 | 0 |
| 90 | 0.5587 | 0 | 0 | 0.5940 | 0.0000 | 0 | 0 | 0.0000 | 0.4054 | 0 |
| 120 | 0.4974 | 0 | 0 | 0.5115 | 0.4436 | 0 | 0 | −0.5767 | 0.0890 | 0 |
| 150 | 0.2471 | 0 | 0 | 0.2012 | 0.4416 | 0 | 0 | −0.3871 | −0.4215 | 0 |
| 180 | 0.1670 | 0 | 0 | 0.0000 | 0.4193 | 0 | 0 | 0.0000 | −0.6448 | 0 |
| ... | ... | ... | ... | ... | ... | |||||
| 10000/T | T | Q |
| 50 | 200 | 2.4981113 |
| 40 | 250 | 2.9310031 |
| 33.557047 | 298 | 3.3027287 |
| 33.333333 | 300 | 3.3174545 |
| 28.571429 | 350 | 3.6689322 |
| 25 | 400 | 3.9930044 |
| 22.222222 | 450 | 4.2949329 |
| 20 | 500 | 4.5785312 |
| 16.666667 | 600 | 5.1015135 |
| 14.285714 | 700 | 5.5780156 |
| 12.5 | 800 | 6.0183203 |
| 11.111111 | 900 | 6.4294505 |
| 10 | 1000 | 6.8164426 |