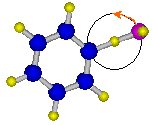
Fig. QS2-1. "Wagging" vibraion of H-abstraction TS of OH + benzene.
Having succeeded to run BEx1D tools, let us investigate the sample input and ouput files in detail in the next three steps.
Sample problem 1: wagOHbenTSabs

bx1fitPlls input: wagOHbenTSabs.fit
'#' is a title line:# CH-OH wag of OH + benzene H abstraction TS (mass weighted coordinate)
outputOption powerSerieswhich tells bx1fitPlls to generate input file for bx1VIBsol named
'wagOHbenTSabs.inp'. Note that bx1VIBsol only
accept power series potential and the regression function defined
in the following block must be a power series.
optFuncs{
const
pow 2
pow 4
pow 6
pow 8
pow 10
pow 12
}
defines the regression function. The key 'const'
stands for a constant term, and 'pow n' means
xn. Thus, this example is a
polynomial;
y = a0
+ a1x2
+ a2x4
+ a3x6
+ a4x8
+ a5x10.
xyTable{
0. 0.
0.175395353 40.11886525
0.354069718 189.0859545
0.538962708 521.7658202
0.73251983 1134.26377
0.936579205 2136.432343
1.152654481 3654.297605
1.382347157 5833.785823
1.627451293 8827.658145
1.889951279 12732.18273
}
where each line in the block beginning with 'xyTable{' terminating
by '}' contains one datum point, in the order of x (coordinate)
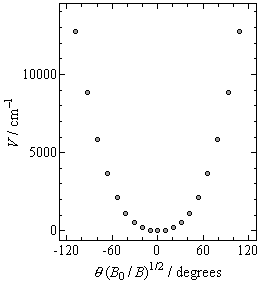
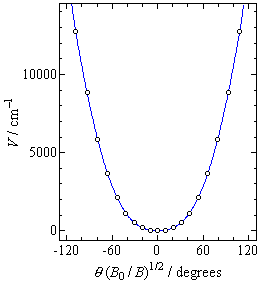
and y (potential energy). As shown in Fig. QS2-2, the
potential energy curve is anharmonic.
continue{
numBasis 501 ! number of basis functions
rotConst 1.89349 ! rotational constant [cm-1]
hoFreq 73.3072 ! harmonic oscillator frequency [cm-1]
!
! output vector ! (and/or function)
!
tempRange 300 570 30
tempRange 600 950 50
tempRange 1000 2000 100
}
Any line in this block is merely copied to the bx1VIBsol input,
'wagOHbenTSabs.inp'. Although bx1fitPlls neither
reads nor checks the contents of this block, they must be proper
input for bx1VIBsol.bx1fitPlls console output
'wagOHbenTSabs.inp'. Other
diagnostic messages and related statistics are printed to the console.===== results of linear least squares regression ===== Function: y = a0 + a1 * x^2 + a2 * x^4 + a3 * x^6 + a4 * x^8 + a5 * x^10 + a6 * x^12The parameters to be optimized are numbered consecutively,
a0, a1, a2, ..., as they
appear in the optFuncs block.Optimum parameters (+-) standard deviations (relative) a0 = -1.0306367e+000 (+-) 1.3167189e+000 ( 127.76 %) a1 = 1.2877844e+003 (+-) 2.0212666e+001 ( 1.57 %) a2 = 2.0746208e+003 (+-) 7.4216348e+001 ( 3.58 %) a3 = -1.2492067e+003 (+-) 1.0363676e+002 ( 8.30 %) a4 = 5.3098393e+002 (+-) 6.5249151e+001 ( 12.29 %) a5 = -1.2179626e+002 (+-) 1.8647156e+001 ( 15.31 %) a6 = 1.1063236e+001 (+-) 1.9588634e+000 ( 17.71 %)show the optimum parameters and their estimated errors.
Parameter correlation coefficients
a0 a1 a2 a3 a4 a5
a1 -0.68038
a2 0.53582 -0.95926
a3 -0.46231 0.90454 -0.98652
a4 0.41867 -0.85999 0.96386 -0.99420
a5 -0.39058 0.82631 -0.94249 0.98355 -0.99721
a6 0.37162 -0.80129 0.92476 -0.97281 0.99186 -0.99858
wagOHbenTSabs.inpwagOHbenTSabs.fit:# CH-OH wag of OH + benzene H abstraction TS (mass weighted coordinate)
continue
block contents:numBasis 501 ! number of basis functions rotConst 1.89349 ! rotational constant [cm-1] hoFreq 73.3072 ! harmonic oscillator frequency [cm-1] ! ! output vector ! (and/or function) ! tempRange 300 570 30 tempRange 600 950 50 tempRange 1000 2000 100In this example, number of basis functions (
numBasis)
is 501, meaning that the harmonic oscillator basis functions (so-called
Hermite-Gaussian functions) for quantum number 0 to 500 are used as
the expansion basis. The next key, rotConst (or
equivalently, hbar2/2m), sets the rotational constant
( = hoFreq, the harmonic
oscillator frequency, input.output key input. This key controls
the output of bex1VIBsol.
potPars{ ! potential parameters
0 -1.0306367
2 1287.7844
4 2074.6208
6 -1249.2067
8 530.98393
10 -121.79626
12 11.063236
}
Each line in the block specifies the order ni and
coefficient ai for the power series term,
aixni. 'wagOHbenTSabs_eigen_values.csv' (eigen values) and
'wagOHbenTSabs_part_funcs.csv' (partition functions).
Optionally, by setting the output key in the input,
'wagOHbenTSabs_eigen_vectors00.csv' (eigen vectors)
and 'wagOHbenTSabs_eigen_funcs00.csv' (eigen functions)
will be also created.
| number | eigenValue | w |
| 0 | 50.340893 | (1/1) |
| 1 | 156.5024 | (1/1) |
| 2 | 268.75298 | (1/1) |
| 3 | 385.86919 | (1/1) |
| 4 | 507.03996 | (1/1) |
| 5 | 631.67864 | (1/1) |
| 6 | 759.33796 | (1/1) |
| 7 | 889.66457 | (1/1) |
| 8 | 1022.3721 | (1/1) |
| ... | ... | ... |
| 10000/T | T | Q |
| 33.333333 | 300 | 1.882205 |
| 30.30303 | 330 | 2.0603718 |
| 27.777778 | 360 | 2.2366488 |
| 25.641026 | 390 | 2.4112197 |
| 23.809524 | 420 | 2.5842349 |
| ... | ... | ... |