Sample problem 3: c2h2TSbendHH

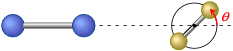
Fig. 4-1. ω₄ bending vibration of the transition state of C₂(X) + H₂ reaction.

bx1fitPlls input:  c2h2TSbendHH.fit

1. The first two non-blank lines are similar to the previous two samples.   The line beginning with '#' is a title line and next non-blank line is an output option control.

   # H2 internal rotation of C2(X) + H2 TS
   
   outputOption powerSeries

   which tells bx1fitPlls to generate input file for bx1S2HRsol.   The program bx1S2HRsol requires potential function in the power series of z = cos(θ).
2. The first block;

   optFuncs{
     const
     pow   2
     pow   4
     pow   6
     pow   8
     pow  10
     pow  12
   }

   tells bx1fitPlls that the regression function is:   V = a₀ + a₁ z² + a₂ z⁴ + a₃ z⁶ + ... + a₆ z¹².
3. Next block is a potential data table:

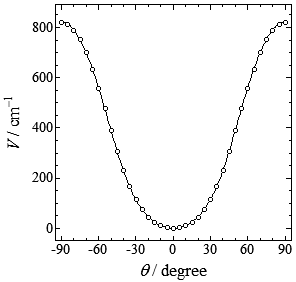
   xyTable{
     1.          0.
     0.996195    2.596
     0.984808   10.579
     0.965926   24.539
     0.939693   45.493
     0.906308   74.887
     0.866025  114.480
     0.819152  165.960
     0.766044  230.224
     0.707107  306.259
     0.642788  390.305
     0.573576  476.646
     0.5       559.638
     0.422618  634.982
     0.342020  699.740
     0.258819  751.938
     0.173648  790.227
     0.087156  813.656
     0.        821.564
   }

   Each line between block header 'xyTable{' and terminator '}' defines a datum point with the simple two-column format as explained in the first sample.   Figure 4-2 shows the potential energy curve along θ.
   
   Fig. 4-2. Potential energy curve along θ.
4. The last block is a 'continue' block:

   continue{
     maxJ      70        ! maximum J
     rotConst  54.0077   ! for H2 / cm-1
     nuSpinSt  2  1 3    ! period = 2, alternation is 1,3,1,3,... (H2)
     !rotConst  27.1731   ! for D2 / cm-1
     !nuSpinSt  2  2 1    ! period = 2, alternation is 2,1,2,1,... (D2)
     !symNumbr  2         ! might be specified instead of nuSpinSt
     !
     !output all
     !
     tempList 290 300 350 400 450 500
   }

   Any line in the block is copied to the bx1S2HRsol input, 'c2h2TSbendHH.inp'.

bx1fitPlls console output

bx1S2HRsol input:  c2h2TSbendHH.inp

1. The first line is a title line copied from c2h2TSbendHH.fit:

   # H2 internal rotation of C2(X) + H2 TS

2. Also, following non-blank lines are copy of continue block contents:

   maxJ      70        ! maximum J
   rotConst  54.0077   ! for H2 / cm-1
   nuSpinSt  2  1 3    ! period = 2, alternation is 1,3,1,3,... (H2)
   !rotConst  27.1731   ! for D2 / cm-1
   !nuSpinSt  2  2 1    ! period = 2, alternation is 2,1,2,1,... (D2)
   !symNumbr  2         ! might be specified instead of nuSpinSt
   !
   !output all
   !
   tempList 290 300 350 400 450 500

   i) 'maxJ', is the maximum rotational quantum number in the expansion basis.
   ii) 'rotConst' sets the rotational constant ( = ² / 2I ).
   iii) 'nuSpinSt' or 'symNumber' are similar to the previous sample.
   iv) The keys output, tempList, etc. can be used similarly to the previous two samples.
3. The last part is potential function input similar to the first sample.

   potPars{           ! potential parameters
     0   821.67758
     2   -1053.3809
     4   242.56772
     6   -1654.8564
     8   3764.0737
     10   -2852.4891
     12   732.34203
   }

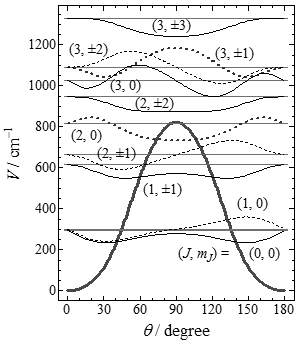
bx1S2HRsol output

The first few eigen values are shown in Fig. 4-3 with eigen functions.

Fig. 4-3. First few eigen values and eigen functions.