Copyright © 1998–2025 by A. Miyoshi
SSUMES - Quick Start step-4
SSUMES - Quick Start step-4
Example problem-4
Next example is the steady-state dissociation problem
of the adducts shown in Fig. Q2. For the multiple-well system,
the solution to the eigenvalue problem (1) is not always the solution
needed.
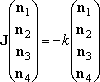
(1)
where,
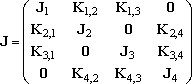
(2)
The solution we want may be the solution of the eq (3), which is the
steady-state dissociation of
well-1 (2-phenylvinyl radical).
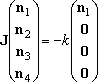
(3)
The solution for this equation can be obtained by iteratively solve the
linear equation (4), starting from an initial guess,
n1(0).
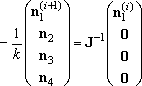
(4)
Control input
The contents of the control input file,
rc2h2ph_m_da.inp,
is shown below.
# phenyl-c2h2 quadruple-well model - dissociation (from all wells)
tempList 1000
pressUnit atm
pressLog10Range -6 6 1
err3 1e-15
well{
index 1
filename rc2h2ph_mw1_mas
offset 27
connect 2 1 ! connect to well-2 via channel-1
connect 3 2 ! connect to well-3 via channel-2
}
well{
index 2
filename rc2h2ph_mw2_mas
offset 23
connect 1 1 ! connect to well-1 via channel-1
connect 4 2 ! connect to well-4 via channel-2
}
well{
index 3
filename rc2h2ph_mw3_mas
offset 71
connect 1 1 ! connect to well-1 via channel-1
connect 4 2 ! connect to well-4 via channel-2
}
well{
index 4
filename rc2h2ph_mw4_mas
offset 0
connect 2 1 ! connect to well-2 via channel-1
connect 3 2 ! connect to well-2 via channel-2
}
Compared to the previous example, the lines beginning with
'recombChan' or
'truncate'
are missing since they are not needed for steady-state dissociation
problem. The line beginning with
'err3' specifies
cut-off of the collisional energy transfer probability which determines
the band-width of the matrix of the master-equation.
Solving master-equation for dissociation
by an eigenvalue problem solver
- Run diseig as:
(This may take a few minutes.)
diseig rc2h2ph_m_da > rc2h2ph_m_da_diseig.log
- The program diseig gives solution to the eigenvalue problem (1)
as the least-negative eigenvalue.
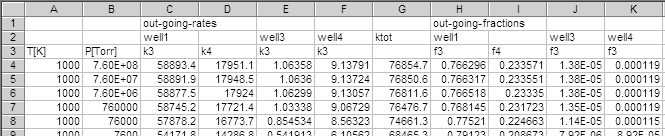
A part of the results is shown below.
These are the rate of dissociation of a kind of mixture of four
intermediates.
Solving master-equation for dissociation
by an iterative linear equation solver
- Run dislit as:
(This may also take a few minutes.)
dislit rc2h2ph_m_d1 > rc2h2ph_m_d1_dislit.log
- The program dislit gives solution to the problem (3)
by iterative procedure (4).
A part of the results is shown below.
Note that the total rate constant,
(
'ktot'), are different from the results obtained by
the eigenvalue problem solver, diseig.
- Run dislit as:
(This may also take a few minutes.)
dislit rc2h2ph_m_d4 > rc2h2ph_m_d4_dislit.log
- In this example, the solution to eq (5) is calculated by dislit.
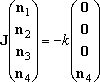
(5)
A part of the results is shown below.
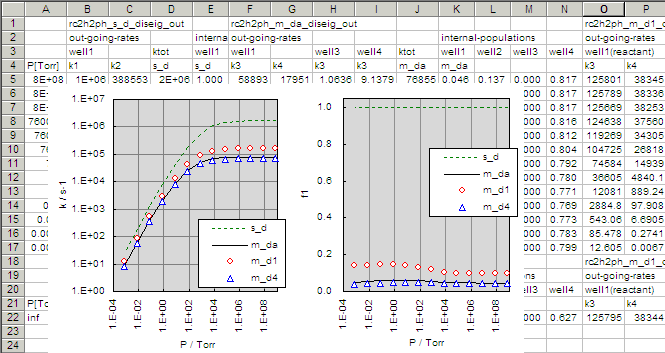
- The results including that in example-2 are summarized in the plots below.
- The solution to eq (3),
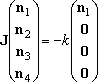
(3)
is the steady-state dissociation of well-1 (2-phenylvinyl), under
the condition that only 2-phenylvinly is produced but there is sufficiet
time to maintain the steady-state population of this molecule.
Even in this case, the rate of dissociation is much smaller than the solution
obtained in the example-2 where the all the other wells are ignored.
But it is larger than the steady-state solution obtained by diseig
for a kind of steady-state mixture of four wells. These results can be
understood by lookin at the steady-state population fractions in wells.
The right plot for 'f1' shows the fraction of population in
well-1. Even when the 2-phenylvinyl is produced in the system,
there are wells more stable than it, and the buffering effect reduces
the steady-state population in well-1, resulting in the smaller overall
dissociation rate.
- Similarly, the solution to eq (5),
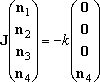
(5)
is the steady-state dissociation of well-4 molecule.
- For the multiple-well system with fairly high barriers, as this example,
the independent solutions to each well are known to be able to reproduce
the phenomena. [N. Yamauchi, A. Miyoshi, K. Kosaka, M. Koshi, and H. Matsui,
J. Phys. Chem. A, 103, 2723–2733 (1999).].
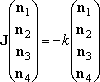 (1)
(1)
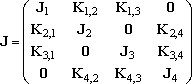 (2)
(2)
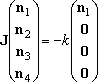 (3)
(3)
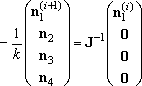 (4)
(4)
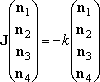 (1)
(1)
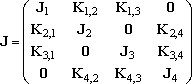 (2)
(2)
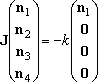 (3)
(3)
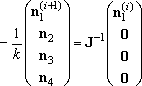 (4)
(4)

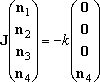 (5)
(5)

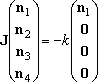 (3)
(3)
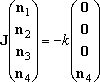 (5)
(5)