SSUMES - Quick Start step-2

SSUMES - Quick Start step-2

Example problem-2

The next example is the steady-state thermal decomposition of 2-phenylvinyl radical which is the adduct shown in Fig. Q1. The same MASTER input file as example-1, rc2h2ph_s_mas.dat, will be used with slightly different control input file, rc2h2ph_s_d.inp.

Control input

The contents of the control input file, rc2h2ph_s_d.inp, is shown below.

# phenyl-c2h2 single-well model - dissociation

tempList 1000
pressUnit atm  ! change the pressure unit to 'atm'
pressLog10Range -6 6 1
output HPL

well{
  filename rc2h2ph_s_mas
}

It is similar to rc2h2ph_s_ca.inp in the previous example, but it lacks lines beginning with 'recombChan' and 'truncate' which are not necessary for the steady-state dissociation problem. Also, in this case, pressure is scanned for a single temperature, 1000 K, whereas, temperature is scanned in the previous example.

Solving master-equation for dissociation problem

Run diseig as:
diseig rc2h2ph_s_d > rc2h2ph_s_d_diseig.log
Find three new files in the current directory. The file, rc2h2ph_s_d_diseig.log, contains diagnostic messages, rc2h2ph_s_d_diseig_hpl.csv contains the high-pressure limiting rate coefficients, and the file, rc2h2ph_s_d_diseig_out.csv, contains the essential results of calculations, part of which is shown below:
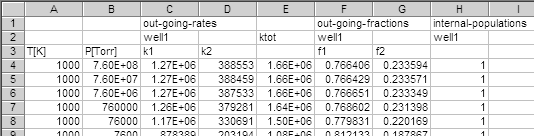
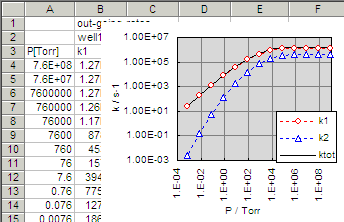
The columns k1 and k2 shows the rate coefficients for the thermal decomposition of 2-phenylvinyl radicals to phenylacetylene + H (k₁) and phenyl radical + C₂H₂ (k₂), respectively. As described in the previous example, the channels are ordered from one with lowest E₀ to higher. The fall-off pressure dependence of the rate coefficients looks like:

[Top] < Prev Step | Next Step >