Using Octave

GNU Octave は John W. Eaton らによって開発された科学技術計算用の高級プログラミング言語 (フリーウェア) です. この解説は 2018 年 3 月現在の Octave 4.2.2 に基づいています. 改良やアップデートによって最新のバージョンと異なる場合がありますが, その場合はご容赦下さい.

Octave の入手とインストール

公式サイトに各種 OS (GNU/Linux. macOS, BSD, Windows) 用の入手方法・インストール方法がまとめられています.

マニュアル

公式マニュアルを参照して下さい. ここ 10 年ほどの間にユーザも増えてきて web 検索で答えが見つかることも多くなっています.

起動と終了

ショートカットなどから起動するか, コマンドラインで octave↵ と入力することで起動します.
```
GNU Octave, version 4.2.2
Copyright (C) 2018 John W. Eaton and others.
 :
>>
```
Octave のプロンプト ( >> ) で exit↵ または quit↵ と入力することで Octave は終了します. 下線は入力部分, "↵" は [Enter] キーを表します.
```
>> exit↵
```
無限ループに入ったり, 予想外に時間のかかる計算を実行してしまった時などは [Ctrl]-c ([Ctrl] を押しながら [c] を押すこと) で実行を停止することができます.

インタラクティブな使い方

Octave を起動し, 以下のような計算式を入力してみましょう.
```
>> 2.3 * exp(-0.23 * 2)↵
ans =  1.4520
```
- Windows のコマンドプロンプトや UNIX のシェルと同様に, カーソルキー [↑], [↓] を使って過去の入力履歴を呼び出して, 編集・再実行することができます.
- 直前の答えは変数 ans に格納されていて再利用できます.
- 出力の桁数を増やしたいときは format long↵ と入力します. output_precision(12)↵ のように有効桁数を指定することもできます.
```
>> 5 * ans↵
ans =  7.2598
>> format long↵
>> ans↵
ans = 7.25976192332965
>> output_precision(12)↵
>> ans↵
ans =  7.25976192333
```
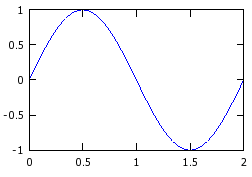
以下のように入力してみましょう. 下に示すようなプロットができるはずです. このように式の値や関数の形状を確認しながら, ステップ-バイ-ステップに計算を進めることができるのが Octave の特徴です.
```
>> x = 0:0.01:2;↵
>> plot (x, sin(pi*x));↵
```

スクリプトの実行

もちろん Octave はファイルに記述されたプログラムを, 一気に実行することもできます. 以下のような内容のテキストファイル mysource.m を Octave を実行しているカレントディレクトリに作成して下さい.
```
x = 1:10
sum(x)
```
そして Octave のプロンプトから以下のように入力するとプログラムが実行されます.
```
>> mysource↵
x =
    1    2    3    4    5    6    7    8    9   10
ans =  55
```
同じことは source 関数でもできます. 上との違いはファイル名の拡張子が .m でなくてもよいことだけです.
```
>> source mysource.m↵
```
Octave のプロンプトから edit 関数でテキストエディターを起動することができます.
```
>> edit mysource.m↵
```
これまでに Octave で入力したコマンドの履歴を利用して, スクリプトファイルを作成することもできます. 入力行履歴はファイル ~/.octave_hist (WSL を含む Linux) あるいは C:\Users\ユーザ名\.octave_hist (Windows) に格納されています.

行列・ベクトル

行列・ベクトルは, 行の区切りにセミコロン ";" を, 行内の列区切りに空白 " " またはカンマ "," を用い, 角括弧 [ ] でくくって表現します. 以下の例では, 連立一次方程式 Ax = b を解いています.
```
>> A = [2, 1; 1, 3]↵
A =
   2   1
   1   3
>> b = [3; 4]↵
b =
   3
   4
>> x = A \ b↵
x =
   1.00000
   1.00000
```
逆行列を計算する inv() 関数や転置行列を表す後置演算子 ' などを用いて様々な線形演算を行うことができます.
```
>> inv(A)↵
ans =
   0.60000  -0.20000
  -0.20000   0.40000
>> b'↵
ans =
   3   4
>> b' * b↵
ans =  25
>> det(A)↵
ans =  5.0000
```
以下の例では, 行列の固有値と固有ベクトルを計算しています. 計算結果の固有値は行列 lambda の対角要素として大きい順に格納されており, 固有ベクトルは行列 vec に縦ベクトルとして固有値の順に格納されています。
```
>> A = [-1, 1; 1, -1]↵
A =
  -1   1
   1  -1
>> [vec, lambda] = eig(A)↵
vec =
   0.70711   0.70711
  -0.70711   0.70711
lambda =
Diagonal Matrix
  -2   0
   0   0
```

微分方程式

Octave には常微分方程式のソルバとして LSODE が実装されています. 下の例では, 逐次反応 A → B (1), B → C (2) を記述する, 次の連立微分方程式を解いています.
d[A]/dt = −k₁[A]
d[B]/dt = k₁[A] − k₂[B]
d[C]/dt = k₂[B]

解くべき微分方程式を関数 f として定義します.

>> function xdot = f(x, t)↵
  xdot(1) = -5 * x(1);↵
  xdot(2) =  5 * x(1) - 1 * x(2);↵
  xdot(3) =             1 * x(2);↵
endfunction↵

初期条件 x0 と出力時間 t を設定します. linspace は一定間隔の数値の並び (横ベクトル) を生成する関数です.
```
>> x0 = [1; 0; 0];↵
>> t = linspace(0, 3, 31)';↵
```
lsode を呼び出して数値解を計算します.
```
>> xout = lsode("f", x0, t);↵
```

計算結果を, 第一列に時間 t を追加して出力します. format は出力書式を設定する関数です. [t, xout] は縦ベクトル t と同じ行数の行列 xout を連結した行列です.

>> format short;↵
>> [t, xout]↵
ans =
   0.00000   1.00000   0.00000   0.00000
   0.10000   0.60653   0.37288   0.02059
     :         :         :         :
   3.00000   0.00000   0.06223   0.93777

計算結果をプロットします.
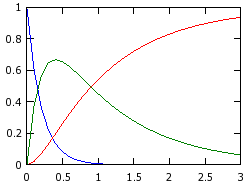
```
>> plot(t, xout)↵
```

非線形方程式

Octave には非線形方程式を解くための fsolve 関数が用意されています. 下の例では, 次の非線形方程式を解いています.
f(x) = 1×10¹³ x^−1.39 exp(−17921 / x) − 1 = 0

解くべき非線形方程式が f(x) = 0 となるように, 関数 f を定義します.

>> function y = f(x)↵
>   y = 1e13 * x^(-1.39) * exp(-17921/x) - 1;↵
> endfunction↵

解の初期推定とともに fsolve を呼び出して解を得ます.

>> [x, fval, info] = fsolve("f", 800)↵
x =  873.34
fval = 9.4820e-007
info =  1

例：Gray-Scott モデル

以下は, Gray-Scott モデルと呼ばれる反応拡散方程式を単純な陽解法で解く Octave プログラムです.
gray_scott.m
右クリックでダウンロードしたら, カレントディレクトリにおいて実行してみて下さい.
```
>> gray_scott↵
```
カレントディレクトリが, どこだかわからない場合は pwd↵ と入力してみて下さい.
```
>> pwd↵
ans = C:\Users\myaccount
```

Octave を使う - Octave 入門