Using NASA-CEA
A. Miyoshi
A. Miyoshi
The CEA is a computer program for chemical equilibrium calculation developed by Dr. S. Gordon, Dr. B. J. McBride, and co-workers in NASA Glenn Research Center. It contains a thermodynamic data library, the PAC99 program which does regression and estimation of thermodynamic data, etc., as well as the main chemical-equilibrium code (CEA2).
 Using CEA from Command Prompt
Using CEA from Command Prompt CH4_O2_N2_tp.inp
(Right-click to download)
CH4_O2_N2_tp.inp
(Right-click to download)problem tp p(atm) = 1 3 t(k) = 300 350 900 2000 reactant name = CH4 moles = 0.11 name = O2 moles = 0.21 name = N2 moles = 0.79 end
tp).
Calculations are done for eight combinations of pressures (1 and 3 atm)
and temperatures (300, 350, 900, and 2000 K).
prob[lem] and reac[tant]
indicate the beginning of the input blocks for the conditions except for the
reactant composition and for the reactants.
Since the calculations were done assuming the ideal gas, two state variables
which are taken to be constants must be specified by their symbols.
In this example, the temperature (t) and the pressure
(p) is held constant. Other variables may also be
specified, for example, hp (constant enthalpy and pressure
= isobaric adiabatic), uv (constant internal energy and volume
= isovolume adiabatic), and etc.
moles) or weights (wt).
Unlike the mole fractions or weight percent, the sum needs not to be unity
or one hundred.
"THERMODYNAMIC EQUILIBRIUM ... PROPERTIES AT ASSIGNED".
An extract is shown below.
THERMODYNAMIC EQUILIBRIUM PROPERTIES AT ASSIGNED
TEMPERATURE AND PRESSURE
CASE =
REACTANT MOLES ENERGY TEMP
KJ/KG-MOL K
NAME CH4 0.1100000 0.000 0.000
NAME O2 0.2100000 0.000 0.000
NAME N2 0.7900000 0.000 0.000
O/F= 0.00000 %FUEL= 0.000000 R,EQ.RATIO= 1.047619 PHI,EQ.RATIO= 0.000000
THERMODYNAMIC PROPERTIES
P, BAR 1.0132 1.0132 1.0132 1.0132 3.0397 3.0397 3.0397 3.0397
T, K 300.00 350.00 900.00 2000.00 300.00 350.00 900.00 2000.00
RHO, KG/CU M 1.3484 0 9.6032-1 3.7013-1 1.6648-1 4.1432 0 3.0809 0 1.1104 0 4.9956-1
H, KJ/KG -3290.30 -2962.43 -2263.54 -683.63 -3321.66 -3061.66 -2263.55 -688.02
U, KJ/KG -3365.44 -3067.94 -2537.30 -1292.25 -3395.03 -3160.33 -2537.31 -1296.51
G, KJ/KG -5210.59 -5559.99 -10010.3 -20168.8 -5129.20 -5445.26 -9709.59 -19500.2
S, KJ/(KG)(K) 6.4010 7.4216 8.6076 9.7426 6.0251 6.8103 8.2734 9.4061
M, (1/n) 33.194 27.581 27.335 27.323 33.998 29.495 27.335 27.328
MW, MOL WT 27.339 27.581 27.335 27.323 27.335 27.503 27.335 27.328
(dLV/dLP)t -1.03649 -1.00001 -1.00000 -1.00026 -1.01180 -1.17474 -1.00001 -1.00013
(dLV/dLT)p 1.6437 1.0002 1.0000 1.0090 1.2079 3.5514 1.0001 1.0046
Cp, KJ/(KG)(K) 4.2185 1.1279 1.3161 1.6012 2.2991 11.7487 1.3162 1.5554
GAMMAs 1.1415 1.3649 1.3006 1.2395 1.1674 1.1466 1.3006 1.2458
SON VEL,M/SEC 292.9 379.5 596.7 868.6 292.7 336.4 596.7 870.7
MOLE FRACTIONS
CH4 0.00007 0.00450 0.00000 0.00000 0.00001 0.00307 0.00000 0.00000
*CO 0.00000 0.00000 0.00330 0.01235 0.00000 0.00000 0.00330 0.01220
*CO2 0.08937 0.09460 0.09491 0.08582 0.08929 0.09292 0.09491 0.08599
*H 0.00000 0.00000 0.00000 0.00013 0.00000 0.00000 0.00000 0.00007
*H2 0.00000 0.00003 0.01455 0.00597 0.00000 0.00001 0.01454 0.00589
H2O 0.02872 0.18917 0.18188 0.19008 0.00935 0.12677 0.18188 0.19032
NH3 0.00000 0.00001 0.00000 0.00000 0.00000 0.00000 0.00001 0.00000
*NO 0.00000 0.00000 0.00000 0.00014 0.00000 0.00000 0.00000 0.00008
*N2 0.70545 0.71170 0.70536 0.70497 0.70537 0.70969 0.70536 0.70515
*O 0.00000 0.00000 0.00000 0.00001 0.00000 0.00000 0.00000 0.00000
*OH 0.00000 0.00000 0.00000 0.00045 0.00000 0.00000 0.00000 0.00026
*O2 0.00000 0.00000 0.00000 0.00008 0.00000 0.00000 0.00000 0.00003
C(gr) 0.00879 0.00000 0.00000 0.00000 0.00891 0.00283 0.00000 0.00000
H2O(L) 0.16760 0.00000 0.00000 0.00000 0.18707 0.06470 0.00000 0.00000
* THERMODYNAMIC PROPERTIES FITTED TO 20000.K
PRODUCTS WHICH WERE CONSIDERED BUT WHOSE MOLE FRACTIONS
WERE LESS THAN 5.000000E-06 FOR ALL ASSIGNED CONDITIONS
*C *CH CH2 CH3 CH2OH
CH3O CH3OH CH3OOH *CN CNN
...
"9.6032-1" found in the density
(RHO, KG/CU M) output of the results for 1.0132 bar and 350 K
is in the special number format used in the CEA for the output of the
maximum digits in limited columns and is equivalent to
"9.6032E-01" (9.6032 × 10−1).
( ) (parentheses) usually mean gas-phase speceis,
H2O(L) means the liquid water, and C(gr) means graphite.
For more accurate information, see the file thermo.inp found
in the folder where the CEA has been installed.
reac dataset
shown below will give the same result as the example input shown above.
name = C(gr) moles = 0.11 name = H2 moles = 0.22 name = NO moles = 0.42 name = N2 moles = 0.58
"Air" which is the mixture of standard dry air
composition (N2 78.084%, O2 20.9476%, Ar .9365%,
CO2 0.0319%).
 CH4air_tp_a.inp
(Right-click to download)
CH4air_tp_a.inp
(Right-click to download)problem tp p(atm) = 1 3 t(k) = 300 350 900 2000 reactant fuel = CH4 moles = 0.11 oxid = Air moles = 1.00 end
name. They may be specified by using
fuel and oxid[ant] as in this example.
Compared to the case using name, no essential difference in
the calculation is expected except for the outputs related to the ratio of
the fuel to oxidant shown below.
O/F= 16.41389 %FUEL= 5.742541 R,EQ.RATIO= 1.050163 PHI,EQ.RATIO= 1.050240(Compare it with the output of example-1, in which
O/F,
%FUEL, and PHI,EQ.RATIO are zero.)
 CH4air_tp_b.inp
(Right-click to download)
CH4air_tp_b.inp
(Right-click to download)prob tp phi(eq.ratio) = 1.05 p(atm) = 1 3 t(k) = 300 350 900 2000 reac fuel = CH4 oxid = Air end
fuel and oxid, the ratio of the fuel(s) and the
oxidant(s) can be specified with phi(eq.ratio).
The part of the output of this example related to the fuel-oxidant ratio is
looks like:
O/F= 16.41764 %FUEL= 5.741306 R,EQ.RATIO= 1.049924 PHI,EQ.RATIO= 1.050000
 CH4air_tp_c.inp
(Right-click to download)
CH4air_tp_c.inp
(Right-click to download)prob tp phi(eq.ratio) = 1.05 p(atm) = 1 3 t(k) = 300 350 900 2000 reac fuel = CH4 oxid = Air output trace = 1e-10 end
outp[ut]. The option trace
instructs the CEA to output species with mole fractions greater than or
equal to the assigned value.
(The default is 5E-06 = 5 × 10−6)
Since the value is 1E-10 in this example, all the species found with
mole fractions greater than or equal to 1 × 10−10,
in any set of the pressure and temperature, are printed.
A part of the output of this example is shown below.
It should be noted that the number format also changed to the special CEA format
described in the output of example-1.
MOLE FRACTIONS *Ar 8.3594-3 8.4370-3 8.3583-3 8.3546-3 8.3584-3 8.4097-3 8.3583-3 8.3563-3 CH4 6.857 -5 4.709 -3 5.288 -8 8.665-16 7.266 -6 3.077 -3 4.752 -7 7.427-15 *CO 1.022-11 1.496 -9 3.473 -3 1.289 -2 5.828-12 9.006-10 3.472 -3 1.275 -2 *CO2 8.9170-2 9.4656-2 9.4964-2 8.5502-2 8.9098-2 9.2724-2 9.4965-2 8.5668-2 COOH 0.000 0 2.070-32 1.089-14 3.007 -9 0.000 0 2.337-32 1.886-14 5.188 -9 *H 0.000 0 5.730-33 1.434-11 1.279 -4 0.000 0 2.052-33 8.275-12 7.338 -5
 CH4air_tp_d.inp
(Right-click to download)
CH4air_tp_d.inp
(Right-click to download)prob tp phi(eq.ratio) = 1.05 p(atm) = 1 3 t(k) = 300 350 900 2000 reac fuel = CH4 oxid = Air outp trace = 1e-10 plot p t C(gr) H2O(L) H2O end
plot are printed in a text-format file with the extension
plt (in this example, it is CH4air_tp_d.plt).
The variables p and t mean the pressure and the
temperature, respectively. By indicating the names of the species,
their mole fractions are printed.
Below, the contents of the CH4air_tp_d.plt are shown.
The text-file in this format can be read into softwares like MS-Excel.
When using the modified version for command prompt, FCEA2m.exe,
a file with an extension csv will be also created.
This file can be directly opened by MS-Excel.
# p t C(gr) H2O(L) H2O 1.0132E+00 3.0000E+02 9.2118E-03 1.6748E-01 2.8712E-02 1.0132E+00 3.5000E+02 0.0000E+00 0.0000E+00 1.8870E-01 1.0132E+00 9.0000E+02 0.0000E+00 0.0000E+00 1.8108E-01 1.0132E+00 2.0000E+03 0.0000E+00 0.0000E+00 1.8969E-01 3.0397E+00 3.0000E+02 9.3334E-03 1.8695E-01 9.3430E-03 3.0397E+00 3.5000E+02 3.2418E-03 6.4611E-02 1.2673E-01 3.0397E+00 9.0000E+02 0.0000E+00 0.0000E+00 1.8108E-01 3.0397E+00 2.0000E+03 0.0000E+00 0.0000E+00 1.8993E-01 # p t C(gr) H2O(L) H2O
hp (constant enthalpy and pressure =
isobaric adiabatic) in the prob dataset.
For the reactant mixtures with fuels and air (oxygen), this is so-called
adiabatic flame condition.
 CH4air_hp.inp
(Right-click to download)
CH4air_hp.inp
(Right-click to download)prob hp phi(eq.ratio) = 1.05 p(atm) = 1 3 reac fuel = CH4 t(k)= 298.15 oxid = Air t(k)= 298.15 end
hp in the prob dataset,
the temperature(s) of unburnt gas should be given in the reac
dataset. A part of the output is shown below.
This resut indicate the adiabatic flame temperatures to be 2231 K at 1 atm
and 2249 K at 3 atm.
THERMODYNAMIC PROPERTIES P, BAR 1.0132 3.0397 T, K 2230.98 2249.09 RHO, KG/CU M 1.4929-1 4.4487-1 H, KJ/KG -271.06 -271.06
 C3H6air_hp.inp
(Right-click to download)
C3H6air_hp.inp
(Right-click to download)problem hp p(atm) = 1 phi(eq.ratio) = 1 reac fuel= C3H6,propylene t(k)= 298.15 oxid= Air t(k)= 298.15 end
C3H6,propylene as resistered in the thermo.inp.
The cyclopropane is registered with the name C3H6,cyclo-.
THERMODYNAMIC PROPERTIES P, BAR 1.0132 T, K 2332.68 RHO, KG/CU M 1.4913-1 H, KJ/KG 26.047 U, KJ/KG -653.41 G, KJ/KG -22336.7 S, KJ/(KG)(K) 9.5867 M, (1/n) 28.545 (dLV/dLP)t -1.00405 (dLV/dLT)p 1.1160 Cp, KJ/(KG)(K) 2.4353 GAMMAs 1.1695 SON VEL,M/SEC 891.4 MOLE FRACTIONS *Ar 0.00864 *CO 0.01776 *CO2 0.11144 *H 0.00067 *H2 0.00344 H2O 0.12291 *NO 0.00310 *N2 0.71922 *O 0.00053 *OH 0.00446 *O2 0.00784
 C2H2_hp.inp
(Right-click to download)
C2H2_hp.inp
(Right-click to download)prob hp p(atm) = 1 reac name = C2H2,acetylene t(k)= 298.15 end
THERMODYNAMIC PROPERTIES P, BAR 1.0132 T, K 2849.07 RHO, KG/CU M 1.0633-1 : MOLE FRACTIONS : *H 0.03179 *H2 0.30807 C(gr) 0.64748
uv (constant internal-energy and
volume = constant-volume adiabatic) in the prob dataset.
For the reactant mixtures with fuels and air (oxygen), the result
corresponds to the burnt equilibrium state in a constant-volume adiabatic
vessel. The temperature is higher than the (constant-pressure)
adiabatic flame due to the lack of expansion.
 CH4air_uv.inp
(Right-click to download)
CH4air_uv.inp
(Right-click to download)prob uv phi(eq.ratio) = 1.05 rho(kg/m**3) = 1.1316 reac fuel = CH4 t(k) = 298.15 oxid = Air t(k) = 298.15 end
uv in the prob dataset,
the density or the specific volume (volume per unit mass) should be given.
Here, the density is given by rho.
A part of the output is shown below.
The temperature is higher than the (constant-pressure) adiabatic flame.
THERMODYNAMIC PROPERTIES P, BAR 9.0164 T, K 2601.97 RHO, KG/CU M 1.1316 0 H, KJ/KG 436.17 U, KJ/KG -360.61The density required as an input can be, of courese, calculated by using the ideal gas law, but, it may become time consuming task for the complex mixtures. Alternatively, the density can be obtained by, for example see below, a nearly meaningless calculation.
 CH4air_tp_frozen.inp
(Right-click to download)
CH4air_tp_frozen.inp
(Right-click to download)prob tp phi(eq.ratio) = 1.05 p(atm) = 1 t(k) = 298.15 reac fuel = CH4 oxid = Air only CH4 N2 O2 Ar CO2 end
tp),
but the composition change was avoided by only keyword.
Here, the density in the following output (ρ = 1.1316×100 kg/m3)
was used in the input for the constant-volume adiabatic calculation shown above.
THERMODYNAMIC PROPERTIES P, BAR 1.0132 T, K 298.15 RHO, KG/CU M 1.1316 0 H, KJ/KG -271.07 U, KJ/KG -360.61 G, KJ/KG -2426.74 S, KJ/(KG)(K) 7.2302This output will be used in the following calculation for adiabatic compression.
sv and sp in the
prob dataset will be shown.
Isentropic processes, such as adiabatic compression and expansion,
can be calculated.
In many cases, the compression ratio (or the volume ratio) is known,
and the sv will be used.
However, for example for the core-gas model calculation for the
rapid compression machine experiments, the temperature is estimated
from the measured pressure, and then the sp
will be used.
 CH4air_sv_frozen.inp
(Right-click to download)
CH4air_sv_frozen.inp
(Right-click to download)prob sv phi(eq.ratio) = 1.05 s/r = 0.869588 rho(kg/m**3) = 1.1316 3.3948 11.316 reac fuel = CH4 oxid = Air only CH4 N2 O2 Ar CO2 end
sv is specified in the prob
dataset, the specific entropy (entropy per unit mass) and the
density (or the specific volume) should be given.
Here, the results from the "meaningless" calculation
shown above are used. The specific entropy is given by
the value divided by the universal gas constant,
7.2302/8.31451 = 0.869588.
In this calculation, the states compressed at initial volume,
1/3 volume (three-times density), and 1/10 volume (ten-times density)
are calculated for the methan-air mixture
(which was assumed to be non-reactive).
The specific entropy was conserved as shown below.
THERMODYNAMIC PROPERTIES P, BAR 1.0133 4.6099 23.364 T, K 298.16 452.15 687.46 RHO, KG/CU M 1.1316 0 3.3948 0 1.1316 1 H, KJ/KG -271.05 -102.54 172.01 U, KJ/KG -360.60 -238.34 -34.453 G, KJ/KG -2426.84 -3371.70 -4798.48 S, KJ/(KG)(K) 7.2302 7.2302 7.2302
 CH4air_sp_frozen.inp
(Right-click to download)
CH4air_sp_frozen.inp
(Right-click to download)prob sp phi(eq.ratio) = 1.05 s/r = 0.869588 p(bar) = 1.01325 10 23 reac fuel = CH4 oxid = Air only CH4 N2 O2 Ar CO2 end
sp is given in the prob dataset,
the specific entropy and the pressure must be given.
Similarly to above, the specific entropy input is in the value
divied by the gas constant.
In this calculation, the states compressed to the initial pressure,
10 bar, and 23 bar are calculated for the non-reactive methan-air mixture.
THERMODYNAMIC PROPERTIES P, BAR 1.0132 10.000 23.000 T, K 298.16 554.67 684.81 RHO, KG/CU M 1.1315 0 6.0030 0 1.1183 1 H, KJ/KG -271.06 14.197 168.78 U, KJ/KG -360.60 -152.39 -36.887 G, KJ/KG -2426.81 -3996.18 -4782.51 S, KJ/(KG)(K) 7.2302 7.2302 7.2302
only input,
do NEVER corresponds to the combustion equilibrium states of the compressed
gas mixtures.
For such a calculation, perform uv calculation with initial state
equal to the compressed state. For example, from the 1/10-volume compressed
state of above calculation, the input will be as follows.
prob uv phi(eq.ratio) = 1.05 rho(kg/m**3) = 11.316 reac fuel = CH4 t(k) = 687.46 oxid = Air t(k) = 687.46 end
 CH4steam-reforming_tp.inp
(Right-click to download)
CH4steam-reforming_tp.inp
(Right-click to download)! CH4 steam reforming problem tp p(atm) = 1 t(k) = 400 450 500 550 600 650 700 750 800 850 900 950 1000 1050 1100 1150 1200 reac name = CH4 moles = 1 name = H2O moles = 1 omit C(gr) outp plot p t CH4 H2O CO H2 CO2 end
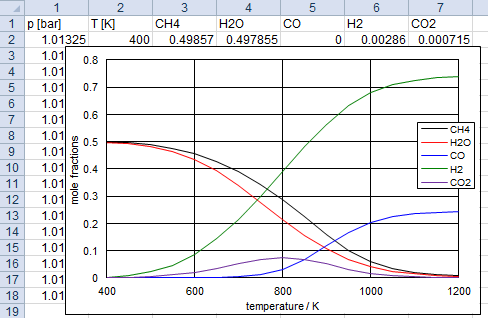
problem tp to this type of problem.
Without this, the calculation will fail at low temperatures because there is
no solution to satisfy the specified pressure.
Also it is essential to set the total pressure to 10 atm.
With 1 atm, no solution could be found at high temperatures where the equilibrium partial
pressure exceeds 1 atm.
 CaCO3_tp.inp
(Right-click to download)
CaCO3_tp.inp
(Right-click to download)! decomposition of CaCO3(cr) problem tp p(atm) = 10 t(k) = 700 750 800 850 900 950 1000 1050 1100 1150 1200 1250 1300 reac name = CaCO3(cr) moles = .9 name = Ar moles = .1 outp plot t p Ar CO2 CaCO3(cr) CaO(cr) end
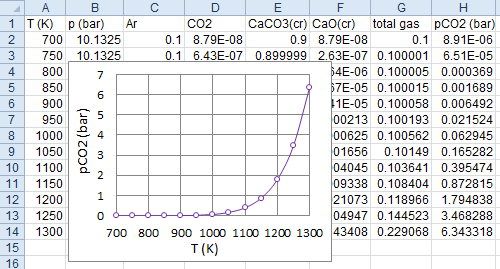
thermo.inp.
 lastpart_of_thermo.inp
(Right-click to download: This is only an example input at around the bottom part,
and cannot be prcessed directly with CEA!)
lastpart_of_thermo.inp
(Right-click to download: This is only an example input at around the bottom part,
and cannot be prcessed directly with CEA!)thermo.inp before END REACTANTS
and add furan as a reactant.
...
RP-1 Mehta et.al. AIAA 95-2962 1995. Hcomb(high) = 19923.BTU/#
0 gll/00 C 1.00H 1.95 0.00 0.00 0.00 1 13.9761830 -24717.700
298.150 0.0000 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.000
C4H4O,furan Furan
0 am1209 C 4.00H 4.00O 1.00 0.00 0.00 0 68.0739600 -34700.000
298.150 0.0000 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.000
END REACTANTS
am1209 in the second line is an optional ID code and may be
left blank. The chemicla formula follows by repeating
[element symbol, number]. The part 68.0739600 is the
molecular weight. The last value in the second line is the standard enthalpy
of formation of gaseous furan (−34.7 kJ mol−1) taken from the
NIST Chemistry WebBook.
The units should be J mol−1. Leave the third line as
this example, usually.
The columns for inputs are read as formated input of FORTRAN, and the column positions
are important.
fcea2.exe or fcea2m.exe, and type thermo (enter).
This name is a special name for thermodynamic database, and this process creates the
new thermo.lib in the current directory.
The procedure below should be done with this new thermo.lib
residing in the current directory.
 furan-air.inp
(Right-click to download)
furan-air.inp
(Right-click to download)problem case=furan-air hp p(atm)=1 phi,eq.ratio=1 reac fuel= C4H4O,furan wt%=100 t(k)= 298.15 oxid= Air wt%=100 t(k)= 298.15 end
thermo.lib, the calculation procedure is exactly the same
as pre-registered compounds.