Copyright © 2004–2025 by A. Miyoshi
BEx1D reference manual - bx1S2HRsol
BEx1D reference manual - bx1S2HRsol
Synopsis
bx1S2HRsol bname
Description
The bx1S2HRsol program solves steady-state
Schrödinger equation for two-dimensional rotor hindered with respect
to the colatitude, θ, only.
For a potential energy curve given by a power series of z (=
cos θ), the eigen states are calculated by expanding the
wavefunction with a two-dimensional free-rotor basis function set,
i.e., the associated Legendre polynomials.
Using the base file name, bname, specified in command-line,
inputs are read from bname.inp and
the eigen-state energies and partition functions are stored in
files bname_eigen_values.csv and
bname_part_funcs.csv, respectively.
Optionally, eigen vectors and corresponding eigen functions can be stored
in bname_eigen_vectors_mJ####_p%%.csv
and bname_eigen_funcs_mJ####_p%%.csv,
respectively, where, #### is the mJ
quantum number and %% is the page number.
Input
The following parameters can be specified in the input file,
bname.inp, for
bx1S2HRsol.
| 1. | title and comments | (*optional) |
| 2a. | solver controls |
| 2b. | solver options | (*optional) |
| 3. | nuclear spin statistics | (*optional) |
| 4a. | output options | (*optional) |
| 4b. | vector/function output control | (*optional) |
| 5. | temperatures for partition function calculation | (*optional) |
| 6. | potential function |
These may appear in any order and as many times as required.
When duplicated, one-value parameter (2, 3, and 4b)
is overwritten by the one appearing later, while duplicated values are
combined to the existing part for multi-value parameter (4a, 5, and 6).
Title: Input line beginning with '#'
followed by at least one white-space character is a title line and
is ignored. A title line differs from a comment line (a line
beginning with '!') in bx1fitPlls input,
but is no longer different in the input for solvers; bx1VIBsol
bx1HRsol, and bx1S2HRsol.
Comment: Any text from an exclamation mark,
'!', to the end of the line is regarded as comments
and ignored. Any blank line, which consists of white-space
characters only, is also skipped by the input parser.
maxJ
maxJ maximum_J_quantum_number
Sets the size of basis-set by the maximum J quantum number.
The basis functions used by
bx1S2HRsol are the latitudinal
part solutions of the two-dimensional free rotor,
i.e., the
associated Legendre functions,
PJm(
z),
with respect to
z (= cos
θ),
where
J = 0, 1, 2, ... and
m = 0, ±1, ...,
±
J.
The following example input tells the program to use basis functions
up to
J = 70.
maxJ 70 ! maximum J
Since the azimuthal part is independent and is the pure one-dimensional
free rotor, the Hamiltonian matrix is diagonalized for each |
m|,
and the size of the matrix is 71 × 71 (
J = 0–70)
for |
m| = 0, 70 × 70 (
J = 0–69) for
|
m| = 1, 69 × 69 (
J = 0–68) for |
m|
= 2, and so on.
rotConst
rotConst hbar-square_over_2I
Specifies the rotational constant,
B (=
 2
2 / 2
I), of the rotor
The unit of
rotConst must be
cm
−1, which is also used as the unit of energy.
precAnal
precAnal [yes | no]
Tells the solver [to perform | not to perform] the precision
analysis. Default is
yes (recommended).
rtolEigen
rtolEigen relative_tolerance
Sets the relative tolerance of the eigenvalues used in the
precision analysis. Default is 0.01 and must be in between
1×10
−6 to 0.1.
Similarly to the free rotation of a symmetric molecule, nuclear
spin statistics need to be properly considered when evaluating the
partition functions. For example, for the two-dimensional hindered
rotation of H
2 in the sample problem described in the
Quick start: step-4,
the rotational states symmetric to the permutation of two identical
hydrogen nuclei (even-
J states) occur only for the antisymmetric
nuclear spin state (para-H
2) with
T (total nuclear spin)
= 0 and thus the statistical weight = 1, while odd-
J states occur
for ortho-H
2 with weight = 3.
The key
nuSpinSt can be used to specify the nuclear
statistical weights. Alternatively, as often used as a good
approximation, the partition function may be calculated with the symmetric
number specified with
symNumbr.
nuSpinSt
nuSpinSt l_period w(1) w(2) ...
w(l_period)
Specifies the periodic alternation of the statistical weight with
J. The first parameter
l_period
specifies the length of the period, followed by the
list of weights.
Below is an example for the internal H
2 rotation in the sample
problem 3. (see
Quick start:
step-4)
nuSpinSt 2 1 3 ! period = 2, 1,3,1,3,... (H2)
!nuSpinSt 2 2 1 ! period = 2, 2,1,2,1,... (D2)
The commented-out second line is for the case of D
2.
symNumbr
symNumbr symmetry_number
Sets a symmetry number for partition-function
calculations.
The
'output' key can be used to control the
outputs. By default, the program creates
output files containing eigen values and partition functions only.
The other output files (eigen vectors and eigen functions) are
created when specified.
output name_of_output-1 [name_of_output-2]
Valid names (
name_of_output-i) are
vector,
function, and
all.
The following three examples are equivalent.
output all
output vector function
output function vector
It should be noted that the calculation of eigen functions often needs much
longer computation
time than that required for the essential calculation, diagonalization of
the Hamiltonian matrix.
Vector/function output control
outJmax
outJmax max-J_for_output
Specifies the maximum
J for eigen vector and eigen function
output. Default is
maxJ × 0.3.
Temperatures for partition function calculation
Temperatures at which the partition functions are calculated
can be specified by any combination of the following three types of input.
tempRange T_start T_end T_step
tempRecipRange numer start end step
tempList T(1) T(2) T(3) ...
The key
tempRange sets an equally spaced temperature list
from
T_start to
T_end, with the interval
T_step.
The next key
tempRecipRange sets a list of temperatures
equally spaced in its reciprocal numbers, that is, they are equally
spaced in Arrhenius plots.
Like a convention used the abscissa of Arrhenius plots, the
reciprocal temperature may be specified in the form like 1000 /
T,
10000 /
T, or
etc. by setting the
numer
(numerator) to 1000, 10000, or
etc. For example,
tempRecipRange 10000 5 40 1
sets a list of temperatures corresponding to 10000 /
T
= 5, 6, 7, ..., 40. The last ley
tempList sets a list of
temperatures as they listed. The temperature input may appear as many time as
requested. For example, the following input is valid.
tempList 298.15
tempRange 300 900 100
tempRecipRange 10000 5 10 1
The default (used when no temperature specification is found in the input)
is equivalent to the following input.
tempRange 300. 1500. 100.
The program assumes a power series potential function (in the unit
of cm
−1) with
respect to
z (= cos
θ) in the following format.
potPars{
order-1 coefficient-1
order-2 coefficient-2
order-3 coefficient-3
...
}
The
order-i must be a nonnegative integer.
Output
The results of calculation are stored in the following four types of
files.
| output | file name |
| 1. | eigen values |
bname_eigen_values.csv |
| 2. | partition functions |
bname_part_funcs.csv |
| 3. | eigen vectors |
bname_eigen_vectors_mJ####_p%%.csv |
| 4. | eigen functions |
bname_eigen_funcs_mJ####_p%%.csv |
Eigen vectors and eigen functions are written in a separated file for each
mJ. The output may be further separated to avoid
too many columns in a file. In the file names,
#### is
mJ (
#### =
0000,
0001, ...) and
%% is the page number
(
%% =
00,
01, ...).
Diagnostic messages like below are printed to the console
(standard output).
estimated eigenvalue error is <= 0.01 at number = 2555.
estimated partition function error is 0 at 500 K.
The first message tells the error estimate of the eigen values,
and the second is that for the partition function calculation.
Table r4-1. Eigen value output
| number | eigenValue | J | mJ | w |
| 0 | 293.12637 | 0 | 0 | (1/4) |
| 1 | 300.35343 | 1 | 0 | (3/4) |
| 2 | 613.78495 | 1 | 1 | (3/4) |
| 3 | 662.57054 | 2 | 1 | (1/4) |
| 4 | 815.07134 | 2 | 0 | (1/4) |
| 5 | 946.70714 | 2 | 2 | (1/4) |
| 6 | 1024.1579 | 3 | 0 | (3/4) |
| ... | ... | ... | ... | ... |
| 2555 | 269239.95 | 70 | 70 | (1/4) | (maximum ... |
Eigen value output
A part of the eigen value output for sample problem 3
is shown in Table r4-1.
The third and fourth columns indicate total angular momentum, J,
and its projection to z-axis, mJ.
The fifth column shows the nuclear spin statistical weight.
From the result of the precision analysis, the
maximum reliable eigenvalue is marked.
Table r4-2. Partition function output
| 10000/T | T | Q | Qz |
| 34.482759 | 290 | 0.3478741 | 1.4893972 |
| 33.333333 | 300 | 0.3750047 | 1.5295799 |
| 28.571429 | 350 | 0.52207593 | 1.7420066 |
| 25 | 400 | 0.68661265 | 1.9706678 |
| 22.222222 | 450 | 0.86660431 | 2.2123024 |
| 20 | 500 | 1.0602155 | 2.4644241 |
Partition function output
An example partition function output is shown in Table r4-2.
The first and the second column show reciprocal number of temperatures and
temperatures in K unit, respectively. The third column shows the
calculated values of the partition function without energy shift, while the
fourth column shows the partition function calculated by shifting the energy
of the lowest eigenstate to be zero.
If the estimated error in the partition function exceed the
predefined threshold (1% relative error), the temperature list
is truncated by removing higher temperatures so that the estimate
error does not exceed the threshold at all the temperatures in the
list. When the program removed some temperatures from list,
it print a warning message to the console. The estimated error
at the maximum temperature calculated is printed to the console.
Table r4-3. Eigen vector output
| eigen_values | 5.427492 | 5.561308 | ... | 468.7031 |
| eigen_vectors | vec0 | vec1 | ... | vec21 |
| c0 | 0.7885 | 0 | ... | 0 |
| c1 | 0 | -0.956 | ... | -1.10E-09 |
| c2 | 0.6083 | 0 | ... | 0 |
| c3 | 0 | -0.2927 | ... | 8.10E-09 |
| c4 | 0.09088 | 0 | ... | 0 |
| c5 | 0 | -0.01855 | ... | 4.23E-08 |
| c6 | -0.00169 | 0 | ... | 0 |
Eigen vector output
Table r4-3 shows a part of eigen vector output for
mJ = 0.
Each column shows the coefficients for the basis functions in the
order of the quantum number J (from mJ to
maxJ). The eigen vectors up to outJmax
are printed in the output. The output is separated in multiple
CSV files when the number of eigen vectors exceeds 250.
The solver solves the problem with the normalized form of the
Hamiltonian,
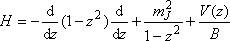 |
(4-1) |
and the eigen values printed in these files are normalized.
The eigen state energies (as reported in the eigen value output) can be
calculated by multiplying the rotational constant,
B.
Table r4-4. Eigen function output
| z | f0 | f1 | ... | f21 |
| -1 | 1.705 | 1.754 | ... | -4.637 |
| -0.980952 | 1.618 | 1.662 | ... | 1.729 |
| -0.961905 | 1.535 | 1.575 | ... | -0.6981 |
| -0.942857 | 1.455 | 1.491 | ... | -1.327 |
| -0.92381 | 1.379 | 1.41 | ... | -0.1898 |
| -0.904762 | 1.306 | 1.333 | ... | 0.9325 |
| -0.885714 | 1.235 | 1.259 | ... | 1.137 |
| ... | ... | ... | ... | ... |
| 1 | 1.705 | -1.754 | ... | 4.637 |
Eigen function output
A part of eigen function output for mJ = 0
is shown in Table r4-4. Each column shows an eigen function
against z (= cos θ) for J =
mJ to outJmax.
The output is separated in multiple
CSV files when the number of eigen functions exceeds 250.
It should be noted that the eigen functions are given for the
Hamiltonian of eq (4-1), i.e., given as a function of z.
In order to obtain the eigen function for the colatitude,
θ, they must be properly converted.
Program limits
Internally,
bx1S2HRsol calls DSBEV routine (eigen
problem solver for real symmetric band matrix) in
LAPACK
written by FORTRAN. Only limitations hard-wired in the source
codes are the declaration part of static arrays which are passed to
FORTRAN routines. These can be found in 'libbx1CP2.h' file
at the beginning of
basisAssocLegendre class
declaration;
class basisAssocLegendre {
public:
enum { MXNBAS = 2001, // maximum number of basis functions
SZWLPK = 6001, // size of DSBEV work array: max(1, 3*MXNBAS-2)
MXRWAB = 51 }; // max nbr rows of DSBEV ab mat: max(maxOrder+1)
that is, the maximum number of the basis functions is 2001 and
the maximum absolute order of the potential function polynomial is 50.
All the other working variables use dynamically allocated memory
and the system resource may limit the program execution.
 2 / 2I), of the rotor
The unit of
2 / 2I), of the rotor
The unit of