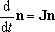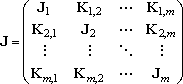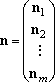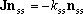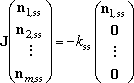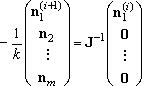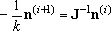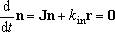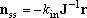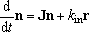For the multiple-well reactions, the steady-state dissociation
described by eq (4) is not always the solution needed.
For the system with fairly high barrier between the isomers (wells),
sometimes, the solution needed is rather represented by,
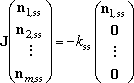 | . (5) |
This corresponds to the situation that the only one isomer (well-1) is
dominantly produced in the reaction system, but the isomerization reactions
are not so fast. The solver,
dislit, calculates the
steady-state distribution,
n1,ss for eq (5) by
iterative procedure, (6), starting from an initial guess,
n1(0).
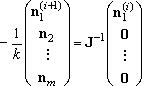 | (6) |
The initial guess is the
Boltzmann distribution for the highest pressure at one temperature,
and the converged vector was used for the initial guess for the next
pressure. Thus the calculation is always done from higher pressure
to lower pressure, and the choice of the starting pressure may affect
the results in some cases.
The
dislit solver is also useful to obtain the steady-state
solution (4). At some condition, especially in the mutiple-well
reactions, the least-negative eigenvalue is not always the solution needed.
This can be observed as the hop of the rate coefficients and
distribution during the pressure scans. For such cases, the iterative
procedure, (7), can be used to obtain the distribution from an initial
guess.
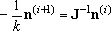 | (7) |
In other words, the distribution thus obtained does not necessarily
correspond to the least-negative eigenvalue.
The LAPACK DSYSV is used to solve the linear equations (6) or (7).