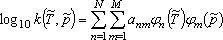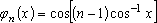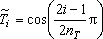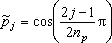Copyright © 1998–2025 by A. Miyoshi
SSUMES reference manual - Chebyshev-polynomial fit
SSUMES reference manual -
Chebyshev-polynomial fit
The RRKM rate coefficients for multiple-well multiple-channel
reactions often show complex temperature and pressure dependences.
The
chebfit program in SSUMES fits the rate coefficients to the
Chebyshev polynomials proposed by Venkatesh
et al.
[
1,
2]
Chebyshev-polynomial Rate Expression
Since the Chebyshev polynomials are defined in [−1, 1]
interval, the ranges of temperature,
T, and pressure,
p;
| Tmin ≤ T ≤ Tmax |
, (1) |
| pmin ≤ p ≤ pmax |
, (2) |
are projected to the [−1, 1] interval as,
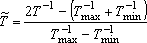 |
, (3) |
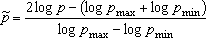 |
. (4) |
It should be noted that the implementation of Chebyshev-polynomial
expression in Chemkin uses the transformation defined by eq. (3)
which is different from the original definition
[
1,
2] which uses the denominator,
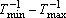
.
The Chebyshev-polynomial expression of the rate coefficients is;
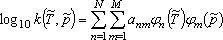 |
. (5) |
Where the Chebyshev polynomial,
φn(
x),
of degree
n − 1 is defined by;
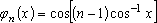 |
. (6) |
The most desirable selection of the rate coefficients for
Chebyshev-polynomial fit is the Gauss-Chebyshev grid defined by;
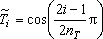 |
, (7) |
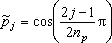 |
. (8) |
where 1 ≤
i ≤
nT and
1 ≤
j ≤
np.
References
| [1] |
P. K. Venkatesh, A. Y. Chang, A. M. Dean, M. H. Cohen, and R. W. Carr,
AIChE J., 43, 1331–1340 (1997). |
| [2] |
P. K. Venkatesh, J. Phys. Chem. A, 104, 280–287
(2000). |
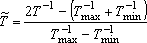
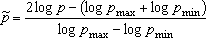
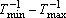 .
.
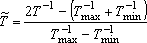
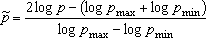
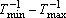 .
.