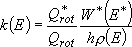[Notes on the eq. 4.1.5]

  Microscopic rate coefficient in the form of eq. (4.1.5);

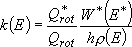      (4.1.5)

may be found in some textbooks and will be used in this lecture for simplicity.

  However, this is not a true microcanonical form since it contains partition functions which are canonical quantities.   This is used for the derivation of the formula for unimolecular rate coefficient, and based on the assumption that the external rotations rapidly relax to the thermal distribution by few collisions.

  A true microcanonical form is eq. (4.1.3);

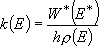      (4.1.3)

including external rotations in the calculation of density and sum of states.   This may be used for some problems, however, is rarely used for the unimolecular reactions since all the energy of external rotations will not be utilized for reaction.

  Probably, the most popular form of the microscopic rate coefficient for unimolecular reactions is eq. (4.1.5').

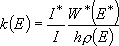      (4.1.5')

This exactly matches with eq. (4.1.5) for 2-dimensional rotors except for the rotational symmetry number, 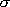, which is omitted since it is same for the reactant and the TS in many cases, but should be properly accounted when needed.

  The eq. (4.1.5') usually implies that the external rotations are seperately considered as a 2D 'inactive' rotation and a 1D 'active' rotation.   The 'inactive' external rotation is a rotation that correlates 2D rotaion of a rotor with two mass points, which approximate two fragments at a large separation.   The 'active' rotation is a rotation around the axis connecting two fragments.   In this case, the 'active' rotation should be considered in the calculation of density and sum of states.
  This is also the case in the J-conservation treatment. So, the rotational energy is approximated by that for 2D rotor (4.1.8), and the evaluation of density and sum of states in eq. (4.1.9) should include the 'active' 1D rotation.

  Sometimes, eq. (4.1.5') is used with the geometric mean of the all the three moments of inertia, although the physical meaning for this is not clear since it does not match with eq. (4.1.5) and the high-pressure limit rate coefficient does not match with the TST.   This approximation (?) usually does not cause serious problem since two moments of inertia will significantly change from reactant to TS but the rest, i.e., that for rotation around the axis connecting two fragment, is expected to be nearly equal for reactant and TS.