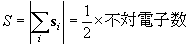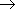 3p 励起) 遷移
3p 励起) 遷移
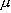 m,
(e) 200
m,
(e) 200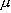 m〜100mm
m〜100mm
| ・電卓を使用してもよい ・ノート・教科書などは持ち込み不可 |
以下の問に答えよ。必要に応じて、 別紙資料の数値・式を参照せよ。
Q1. あるカルボニル化合物のシクロヘキサン溶液 (濃度 52.3 mmol dm-3) の吸収を波長 280 nm で測定した。 光路長 1 cm の吸収セルで透過率は 30.0 % であった。 モル吸光係数 (底 10) を計算し dm3 mol-1 cm-1 の単位でかけ。
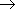 3p 励起) 遷移
3p 励起) 遷移
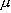 m,
(e) 200
m,
(e) 200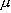 m〜100mm
m〜100mm
Q3. 調和振動子近似で  = 0 と
= 0 と
 = 2 の状態間の赤外振動遷移は禁制である。
この理由を説明せよ。
= 2 の状態間の赤外振動遷移は禁制である。
この理由を説明せよ。
Q4. 二原子分子 AB の J = 0 から J = 1 への吸収が、
波数 33.8 cm-1 に観測された。 これから A-B 結合距離を求めよ
(単位 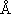 , 1
, 1 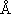 =
10-10 m)。 AB の換算質量は 2.0 amu であり
=
10-10 m)。 AB の換算質量は 2.0 amu であり
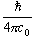 = 16.9 amu
= 16.9 amu
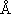 2 cm-1 である。
2 cm-1 である。
Q5. 直線分子の J = 0 と J = 2 の回転状態間の純回転遷移は禁制である。 この理由を説明せよ。 また、二原子分子の純回転遷移は古典回転周波数に、 回転ラマンシフトは古典回転の2倍の周波数に現れる理由を説明せよ。
 3
(反対称伸縮)
3
(反対称伸縮)
 1 (全対称伸縮 =
4つの C-H 結合が同時に伸縮)
1 (全対称伸縮 =
4つの C-H 結合が同時に伸縮)
 1 (対称伸縮振動)
1 (対称伸縮振動)
Q7. Cl 原子には、基底状態 (多重度 4) より 880 cm-1 エネルギーの高い励起状態 (多重度 2) が存在する。 温度 317 K のボルツマン平衡における、 励起状態の基底状態に対する存在比を求めよ。 この温度において kT = 220 cm-1 である (k はボルツマン定数)。
Q8. 同じ温度における、H2, HD, D2 分子の回転分配関数の比を求めよ。
*Q9. 塩素分子 Cl2 の振動の波数は 556
cm-1
である。 温度 400 K の平衡状態において、振動量子数
 = 1 の状態の
= 1 の状態の  = 0
の状態に対する存在比を求めよ。 400 K において kT = 278
cm-1(k はボルツマン定数)であり、
回転定数は振動状態に依存しないとする。
= 0
の状態に対する存在比を求めよ。 400 K において kT = 278
cm-1(k はボルツマン定数)であり、
回転定数は振動状態に依存しないとする。
Q10. 剛体回転子近似のもとで CO 分子 (回転定数 1.92 cm-1) の 303.9 K のボルツマン平衡における回転量子数 J = 10 の状態の回転基底状態 (J = 0) に対する存在比を求めよ。 この温度において kT = 211.2 cm-1 である (k はボルツマン定数)。
*Q11. ある分子の磁気モーメントは 1.73
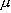 B である
(
B である
(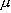 B はボーア磁子)。
磁気モーメントは主に電子スピンによるとして、
この分子の不対電子数を推定せよ。
B はボーア磁子)。
磁気モーメントは主に電子スピンによるとして、
この分子の不対電子数を推定せよ。
1.対数・指数・平方根
| x | 0.1 | 0.2 | 0.5 | 0.7 | 1.5 | 2.0 |
| 自然対数 ln(x ) | -2.30 | -1.61 | -0.69 | -0.36 | 0.41 | 0.69 |
| x | 0.2 | 0.3 | 0.5 | 0.7 | 2.0 |
| 常用対数 log10(x ) | -0.699 | -0.523 | -0.301 | -0.155 | 0.301 |
| x | -4.0 | -2.0 | -1.5 | -1.0 | -0.5 | 0.5 | 1.0 | 1.5 | 2.0 |
| 指数関数 exp(x ) | 0.0183 | 0.135 | 0.223 | 0.368 | 0.607 | 1.65 | 2.72 | 4.48 | 7.39 |
| x | 0.1 | 0.5 | 1.5 | 2.0 | 3.0 | 5.0 | 15.0 |
平方根 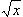 |
0.316 | 0.707 | 1.225 | 1.414 | 1.732 | 2.236 | 3.873 |
2.重要な式
ランベルト-ベール則 (底 10):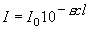 ,
(底 e ):
,
(底 e ): 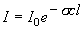
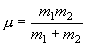
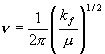
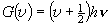 ,
,
 = 0, 1, 2, ...
= 0, 1, 2, ...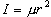
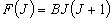 ,
J = 0, 1, 2, ...
,
J = 0, 1, 2, ...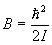 ,
(波数単位):
,
(波数単位): 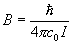
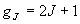
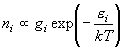
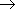 B の平衡定数:
B の平衡定数:
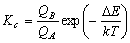
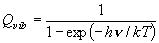
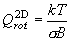
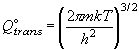 ,
(相対並進):
,
(相対並進): 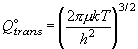
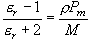 ,
,
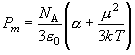
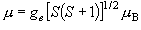 ,
ge = 2.00
,
ge = 2.00