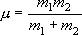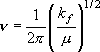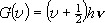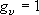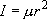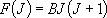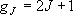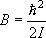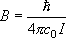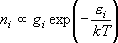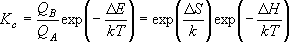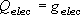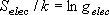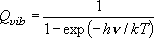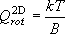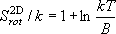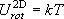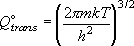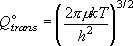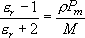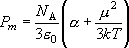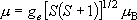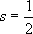= 1 の状態は振動基底状態
(
= 1 の状態は振動基底状態
( = 0 の状態) に対して何%存在するか?
回転定数は振動状態に依存せず、一定であると仮定してよい。
(310.8 K において
= 0 の状態) に対して何%存在するか?
回転定数は振動状態に依存せず、一定であると仮定してよい。
(310.8 K において
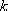
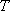 = 216.0
cm-1 である)
= 216.0
cm-1 である)
 1016
molecules cm-3 の気体オゾン (O3) を封入した、
光路長
1 cm の吸収セルで波長 250 nm の吸収を測定したところ、透過率は 50 %
であった。気体オゾンの 250 nm における吸光係数 (吸光断面積; 底は
1016
molecules cm-3 の気体オゾン (O3) を封入した、
光路長
1 cm の吸収セルで波長 250 nm の吸収を測定したところ、透過率は 50 %
であった。気体オゾンの 250 nm における吸光係数 (吸光断面積; 底は
 )
を cm2 (molecule-1) の単位で求めよ。
)
を cm2 (molecule-1) の単位で求めよ。
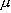 B
であることが分かった
(
B
であることが分かった
(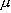 B はボーア磁子)。
磁気モーメントは主に電子スピンによるとして、V(III)
の不対電子数を推定せよ。
B はボーア磁子)。
磁気モーメントは主に電子スピンによるとして、V(III)
の不対電子数を推定せよ。
 )-(
)-(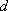 )
の遷移を波長の長い順に並べよ。
)
の遷移を波長の長い順に並べよ。(
 ) H 原子の
Lyman-
) H 原子の
Lyman- 遷移
(電子遷移 : 2p 軌道
遷移
(電子遷移 : 2p 軌道 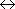 1s 軌道)
1s 軌道)(
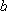 ) HF 分子の純回転遷移
) HF 分子の純回転遷移(
 ) H35Cl 分子の振動遷移
(振動量子数 1
) H35Cl 分子の振動遷移
(振動量子数 1 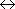 0)
0)(
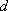 ) D35Cl
(2H35Cl)
分子の振動遷移 (振動量子数 1
) D35Cl
(2H35Cl)
分子の振動遷移 (振動量子数 1 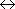 0)
0)
 2
(変角振動)
2
(変角振動)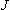 = 16 の状態の
= 16 の状態の
 (
( -
-
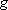 Xelec
= 1, 回転定数
Xelec
= 1, 回転定数 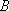 X
= 2.78 cm-1) より 139 cm-1 高エネルギーに励起状態
A (
X
= 2.78 cm-1) より 139 cm-1 高エネルギーに励起状態
A ( AB(A) のエントロピー変化
(
AB(A) のエントロピー変化
(
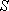 /
/
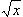
 = 3.14 (円周率)
= 3.14 (円周率)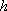 = 6.63
= 6.63 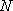 A = 6.02
A = 6.02
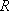 = 8.31 J K-1
mol-1 (気体定数)
= 8.31 J K-1
mol-1 (気体定数)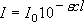
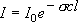
 1,
1,