概要

  統計熱力学の化学平衡 (アトキンス 20 章) の演習問題。

  分子統計力学の基礎となる分配関数の物理的な意味を理解する上で、 分配関数と直接的な関係を持つ量である化学平衡定数との関係は重要である。 この演習は、実際の化学平衡定数の計算を行うことによって、 分子統計熱力学になじむことを目的としている。

図 4-1. 分子 A と B のエネルギー準位

  まず、ボルツマン分布則

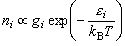
から、化学平衡定数を求めることを考える。分子 A と B のエネルギー準位は、図 4-1 のように定める。分子 A の存在確率は、 A に属するすべてのエネルギー準位の存在確率の和であり、 B に関しても同様であるから、平衡定数は、

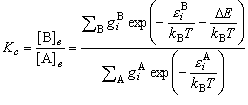
となる。分子の最低のエネルギー状態を基準にした、 ボルツマン分布則による存在確率の和は、分配関数と呼ばれ、Q で表記される。平衡定数を分配関数を使って書き直すと、

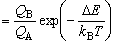
となる。別の表現をすれば、分配関数は「ある温度において、分子が とりうる状態の数」である。

補足説明と演習のヒント

  振動分配関数を評価する場合は、振動準位間隔が cm^-1 で与えられているので、以下の関係を使うとよい。

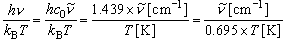
平衡定数の評価では、回転分配関数はあらわに評価しなくても、 その比が評価できればよい。

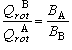
分子の基底状態のエネルギー差は、分光学よりも熱力学測定から得られる ことが多く、単位はモル当たりのエネルギーで与えられることが多い。 一分子あたりのエネルギー差 ΔE, 一モルあたりのエネルギー差を ΔE' とした時、

=

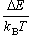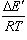
であることに注意せよ。